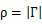א גאַנץ גייד צו VSWR פֿון FMUSER [דערהייַנטיקט 2022]

אין אַנטענע טעאָריע, VSWR איז אַבריוויייטיד פון וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש. 

VSWR איז אַ מעזשערמאַנט פון די שטייענדיק כוואַליע מדרגה אויף אַ פידער ליניע, עס איז אויך באקאנט ווי שטייענדיק כוואַליע פאַרהעלטעניש (SWR). 

מיר וויסן אַז די שטייענדיק כוואַליע, וואָס דערקלערט די שטייענדיק כוואַליע פאַרהעלטעניש, איז אַזאַ אַ וויכטיק פאַקטאָר צו זיין קאַנסידערד פֿאַר ענדזשאַנירז ווען קאַנדאַקטינג רף טעכניש פאָרשונג אויף אַנטענאַז.

כאָטש שטייענדיק כוואליעס און VSWR זענען זייער וויכטיק, אָפט די VSWR טעאָריע און חשבונות קענען מאַסקע אַ מיינונג פון וואָס איז פאקטיש געשעעניש. צומ גליק, עס איז מעגלעך צו באַקומען אַ גוט מיינונג פון די טעמע, אָן דילינג צו דיפּלי אין VSWR טעאָריע.

אָבער וואָס אַקשלי איז VSWR און וואָס טוט עס מיינען פֿאַר בראָדקאַסטינג? דער בלאָג איז די מערסט פולשטענדיק פירער וועגן VSWR, אַרייַנגערעכנט וואָס עס איז, ווי עס אַרבעט און אַלץ איר דאַרפֿן צו וויסן וועגן VSWR. 

זאל ס האַלטן ויספאָרשן!

ייַנטיילונג איז קאַרינג!

1. וואָס איז VSWR? וואָולטידזש שטייענדיק וואַווע פאַרהעלטעניש באַסיקס

1) וועגן VSWR 

-VSWR דעפֿיניציע

וואָס איז ווסוור? פשוט שטעלן, VSWR איז דיפיינד ווי די פאַרהעלטעניש צווישן טראַנסמיטטעד און שפיגלט וואָולטידזש שטייענדיק כוואליעס אין אַ ראַדיאָ אָפטקייַט (רף) עלעקטריקאַל טראַנסמיסיע סיסטעם. 

- אַבריווייישאַן פון VSWR

ווסוור איז אַבריוויייטיד פון וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש, עס איז מאל פּראַנאַונסט ווי "וויסוואַר".

-ווי VSWR וואָרקס

VSWR איז גערעכנט ווי אַ מעזשערמאַנט פון ווי יפישאַנטלי רף מאַכט איז טראַנסמיטטעד - פֿון די מאַכט מקור אוןד דעמאָלט גייט דורך אַ טראַנסמיסיע שורה, און לעסאָף גייט אין די מאַסע.

-VSWR אין בראָדקאַסטינג

ווסוור is געוויינט ווי אַ עפעקטיווקייַט מאָס פֿאַר אַלץ קאַנווייינג רף כולל טראַנסמיסיע שורות, עלעקטריקאַל קייבאַלז און אפילו די סיגנאַל אין די לופט. א פּראָסט ביישפּיל איז אַ מאַכט אַמפּלאַפייער פארבונדן צו אַן אַנטענע דורך אַ טראַנסמיסיע שורה. אַז ס וואָס איר קען אויך באַטראַכטן VSWR ווי די פאַרהעלטעניש פון די מאַקסימום צו מינימום וואָולטידזש אויף אַ אָנווער-ווייניקער שורה.

2) וואָס זענען די הויפּט Fונקטיאָנס פון VSWR?

VSWR זענען וויידלי געניצט אין אַ פאַרשיידנקייַט פון אַפּלאַקיישאַנז, אַזאַ ווי אין אַנטענע, טעלעקאָםמייקראַווייוו, ראַדיאָ אָפטקייַט (RF), עטק 

דאָ זענען עטלעכע פון ​​​​די הויפּט אַפּלאַקיישאַנז מיט דערקלערונג:

אַפּפּליקאַטיאָנס פון VSWR	הויפּט פאַנגקשאַנז פון VSWR
טראַנסמיטינג אַנטענע	די VSWR (Voltage Standing Wave Ratio) איז אַן אָנווייַז פון די סומע פון ​​מיסמאַטש Antenna און די קאָרמען זענען פארבונדן צו אים. דאָס איז אויך באַוווסט ווי די שטייענדיק וואַווע פאַרהעלטעניש (SWR). די קייט פון וואַלועס פֿאַר VSWR איז פֿון 1 צו ∞. א VSWR ווערט אונטער 2 איז גערעכנט ווי פּאַסיק פֿאַר רובֿ אַנטענע אַפּלאַקיישאַנז. די אַנטענע קענען זיין דיסקרייבד ווי אַ "גוטע גלייַכן". אַזוי ווען עמעצער זאגט אַז די אַנטענע איז שוואַך מאַטשט, זייער אָפט עס מיטל אַז די VSWR ווערט יקסידז 2 פֿאַר אַ אָפטקייַט פון אינטערעס.
טעלעקאָממוניקאַטיאָן	אין טעלעקאָממוניקאַטיאָנס, די שטייענדיק כוואַליע פאַרהעלטעניש (SWR) איז די פאַרהעלטעניש פון די אַמפּליטוד פון אַ פּאַרטיייש שטייענדיק כוואַליע אין אַן אַנטיינאָו (מאַקסימום) צו די אַמפּליטוד אין אַ שכייניש נאָדע (מינימום) אין אַן עלעקטריקאַל טראַנסמיסיע ליניע.
מייקראַווייוו	פּראָסט פאָרשטעלונג מיטלען פֿאַרבונדן מיט מייקראַווייוו טראַנסמיסיע שורות און סערקאַץ זענען ווסוור, אָפּשפּיגלונג קאָואַפישאַנט און צוריקקומעןn אָנווער, ווי געזונט ווי טראַנסמיסיע קאָואַפישאַנט און ינסערשאַן אָנווער. די קענען אַלע זיין אויסגעדריקט מיט צעוואָרפן פּאַראַמעטערס, מער קאַמאַנלי ריפערד צו אַ S- פּאַראַמעטערס.
RF	וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש (VSWR) איז דיפיינד ווי די פאַרהעלטעניש צווישן טראַנסמיטטעד און רעפלעקטעד וואָולטידזש שטייענדיק כוואליעס אין אַ ראַדיאָ אָפטקייַט (RF) עלעקטריקאַל טראַנסמיסיע sysהאט. עס איז אַ מעסטן ווי יפעקטיוולי רף מאַכט איז טראַנסמיטטעד פֿון די מאַכט מקור, דורך אַ טראַנסמיסיע שורה און אין די מאַסע

3) לערנען ווי צו עקספּרעסס VSWR פֿון טעכניקער דזשימי

דאָ איז אַ יקערדיק סימפּלאַפייד רף וויסן רשימה צוגעשטעלט דורך אונדזער רף טעכניקער דזשימי. לאמיר לפאַרדינען מער וועגן VSWR דורך די פאלגענדע צופרידן: 

- עקספּרעססינג VSWR ניצן וואָולטידזש

לויט דער דעפֿיניציע, VSWR איז די פאַרהעלטעניש פון די העכסטן וואָולטידזש (די מאַקסימום אַמפּליטוד פון די שטייענדיק כוואַליע) צו די לאָואַסט וואָולטידזש (די מינימום אַמפּליטוד פון די שטייענדיק כוואַליע) ערגעץ צווישן מקור און מאַסע.

VSWR = | V (מאַקס) | / | V (מין) |

V (מאַקס) = די מאַקסימום אַמפּליטוד פון דער שטייענדיק כוואַליע
V (מין) = מינימום אַמפּליטוד פון דער שטייענדיק כוואַליע

- עקספּרעססינג VSWR ניצן אַן ימפּידאַנס

לויט דער דעפֿיניציע, VSWR איז די פאַרהעלטעניש פון מאַסע ימפּידאַנס און מקור ימפּידאַנס.

VSWR = ZL / Zo

ZL = די מאַסע ימפּידאַנס
זאָ = דער מקור ימפּידאַנס

וואָס איז די ידעאַל ווערט פון אַ VSWR?
די ווערט פון אַ ידעאַל ווסוור איז 1: 1 אָדער באַלד אויסגעדריקט ווי 1. אין דעם פאַל, די רעפלעקטעד מאַכט פון די מאַסע צו די מקור איז נול.

- עקספּרעססינג VSWR ניצן אָפּשפּיגלונג און פאָרווערדינג מאַכט

לויט דער דעפֿיניציע איז VSWR גלייך צו

VSWR = 1 + √ (Pr / Pf) / 1 - √ (Pr / Pf)

ווו:

פּר = רעפלעקטעד מאַכט
Pf = פֿאָרווערטס מאַכט

3) פארוואס זאָל איך זאָרגן VSWR? פארוואס איז עס וויכטיק?

די דעפֿיניציע פון ​​VSWR גיט די יקער פֿאַר אַלע VSWR חשבונות און פאָרמולאַס. 

אין אַ פארבונדן שורה, אַ ימפּידאַנס מיסמאַטש קענען אָנמאַכן אָפּשפּיגלונג, וואָס איז פּונקט וואָס עס סאָונדס ווי - אַ כוואַליע באַונסינג צוריק און גיין אין די אומרעכט ריכטונג. 

הויפּט סיבה: די גאנצע ענערגיע ווערט שפיגלט (למשל דורך אַן אָפֿן אָדער קורץ קרייַז) אין די סוף פון די שורה, און קיינער איז נישט אַבזאָרבד, וואָס פּראָדוצירן אַ גאנץ "שטייענדיק כוואַליע" אויף די שורה. 

דער רעזולטאַט פון די אַפּאָוזינג כוואליעס איז אַ שטייענדיק כוואַליע. דאָס פאַרמינערן די מאַכט די אַנטענע נעמט און קענען נוצן צו בראָדקאַסט. עס קען אפילו פאַרברענען אַ טראַנסמיטער. 

די ווערט פון VSWR גיט די מאַכט שפיגלט פֿון די מאַסע צו די מקור. עס איז אָפט געניצט צו שילדערן ווי פיל מאַכט איז פאַרפאַלן פון די מקור (יוזשאַוואַלי אַ הויך פרעקווענסי אַמפּליפיער) דורך די טראַנסמיסיע ליניע (יוזשאַוואַלי אַ קאָאַקסיאַל קאַבלע) צו די מאַסע (יוזשאַוואַלי אַן אַנטענע).

דאָס איז אַ שלעכט סיטואַציע: דיין טראַנסמיטער ברענט אַראָפּ רעכט צו אָוווערכיט ענערגיע.

אין פאַקט, ווען די מאַכט מענט צו זיין שטראַלן קומט צוריק אין די טראַנסמיטער אין פול שטאַרקייַט, עס יוזשאַוואַלי ברענען אויס די עלעקטראָניק דאָרט.

עס איז שווער צו פֿאַרשטיין? דאָ איז אַ בייַשפּיל וואָס קען העלפֿן איר:

אַן אָקעאַן וואַוועטראַין טראַוואַלינג צו ברעג קאַריז ענערגיע צו דעם ברעג. אויב עס לויפט אַרויף אַנטו אַ דזשענטלי סלאָופּינג ברעג, אַלע די ענערגיע געץ אַבזאָרבד, און עס זענען קיין כוואליעס טראַוואַלינג צוריק אָפשאָר. 

אויב אַנשטאָט פון אַ סלאָופּינג ברעג איז אַ ווערטיקאַל סעוואַלל, די ינקאַמינג וואַוועטראַין ווערט גאָר שפיגלט, אַזוי אַז קיין ענערגיע איז אַבזאָרבד אין די וואַנט. 

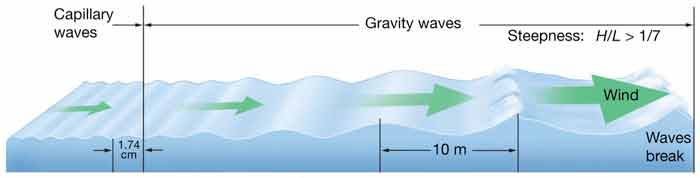
די ינטערפיראַנס צווישן די ינקאַמינג און אַוטגאָוינג כוואליעס אין דעם פאַל פּראָדוצירן אַ "שטייענדיק כוואַליע" וואָס טוט נישט קוקן ווי עס טראַוואַלינג; די פּיקס בלייַבן אין דער זעלביקער ספּיישאַל שטעלעס און נאָר גיין אַרויף און אַראָפּ.

דער זעלביקער דערשיינונג כאַפּאַנז אויף אַ ראַדיאָ אָדער ראַדאַר טראַנסמיסיע ליניע. 

אין דעם פאַל, מיר וועלן אַז די כוואליעס אויף די שורה (סיי וואָולטידזש און קראַנט) צו אַרומפאָרן איין וועג און אַוועקלייגן זייער ענערגיע אין דער געוואלט מאַסע, וואָס אין דעם פאַל קען זיין אַן אַנטענע ווו עס איז צו זיין שטראַלן. 

אויב די גאנצע ענערגיע שפיגלט זיך (למשל, דורך אַ עפענען אָדער קורץ קרייַז) אין די סוף פון די שורה, גאָרניט אַבזאָרבד, וואָס פּראָדוצירן אַ שליימעסדיק "שטייענדיק כוואַליע" אויף די שורה. 

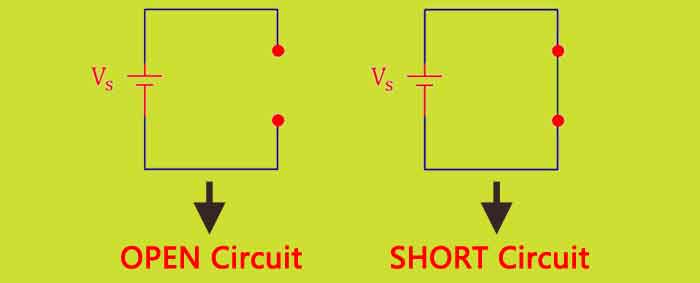
עס טוט נישט נעמען אַ עפענען אָדער קורץ קרייַז צו פאַרשאַפן אַ שפיגלט כוואַליע. כל עס נעמט איז אַ מיסמאַטש אין ימפּידאַנס צווישן די שורה און די מאַסע. 

אויב די רעפלעקטעד כוואַליע איז נישט ווי שטאַרק ווי די פאָרויס כוואַליע, דעמאָלט עטלעכע "שטייענדיק כוואַליע" מוסטער וועט זיין באמערקט, אָבער די נולז וועט נישט זיין אַזוי טיף און ניט די פּיקס ווי הויך ווי פֿאַר אַ גאנץ אָפּשפּיגלונג (אָדער גאַנץ מיסמאַטש).

2. וואָס איז SWR?

1) סוור דעפיניציע

לויט וויקיפּעדיע, די שטייענדיק כוואַליע פאַרהעלטעניש (SWR) איז דיפיינד ווי:

א מאָס פון ימפּידאַנס וואָס ריכטן לאָודז צו די כאַראַקטעריסטיש ימפּידאַנס פון אַ טראַנסמיסיע ליניע אָדער כוואַליע אין ראַדיאָ ינזשעניעריע און טעלאַקאַמיונאַקיישאַנז. SWR איז, אַזוי, די פאַרהעלטעניש צווישן טראַנסמיטטעד און רעפלעקטעד כוואליעס אָדער די פאַרהעלטעניש צווישן די אַמפּליטוד פון אַ שטייענדיק כוואַליע אין זייַן מאַקסימום, צו די אַמפּליטוד בייַ אַ מינימום, SWR איז יוזשאַוואַלי דיפיינד ווי אַ וואָולטידזש פאַרהעלטעניש גערופֿן די ווסוור ".

א הויך SWR ינדיקייץ נעבעך טראַנסמיסיע-שורה עפעקטיווקייַט און שפיגלט ענערגיע, וואָס קענען שעדיקן די טראַנסמיטער און פאַרמינערן די טראַנסמיטער עפעקטיווקייַט. 

זינט SWR אָפט רעפערס צו די וואָולטידזש פאַרהעלטעניש, עס איז יוזשאַוואַלי באקאנט ווי די וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש (VSWR).

2) ווי VSWR אַפעקץ די פאָרשטעלונג פון אַ טראַנסמיטער סיסטעם? 

עס זענען עטלעכע וועגן וואָס VSWR אַפעקץ די פאָרשטעלונג פון אַ טראַנסמיטער סיסטעם, אָדער קיין סיסטעם וואָס קען נוצן רף און מאַטשט ימפּידאַנסיז.

כאָטש דער טערמין VSWR איז נאָרמאַלי געניצט, ביידע וואָולטידזש און קראַנט שטייענדיק כוואליעס קענען גרונט ישוז. עטלעכע פון ​​די אַפעקץ זענען דיטיילד אונטן:

- טראַנסמיטער מאַכט אַמפּלאַפייערז קענען זיין דאַמידזשד

די געוואקסן לעוועלס פון וואָולטידזש און קראַנט געזען אויף די פידער ווי אַ רעזולטאַט פון די שטייענדיק כוואליעס קענען שעדיקן די טראַנסמיטערז פון די טראַנסמיטער. סעמיקאַנדאַקטער דיווייסאַז זענען זייער פאַרלאָזלעך אויב אַפּערייטאַד אין זייער ספּעציפיצירט לימאַץ, אָבער די וואָולטידזש און קראַנט שטייענדיק כוואליעס אויף די פידער קענען אָנמאַכן קאַטאַסטראָפיק שעדיקן אויב זיי פאַרשאַפן די פּלאַן צו אַרבעטן אַרויס זייער לימאַץ.

-פּאַ פּראַטעקשאַן ראַדוסאַז רעזולטאַט מאַכט

ווייַל די זייער פאַקטיש געפאַר פון הויך סוור לעוועלס געפֿירט שעדיקן צו די מאַכט אַמפּלאַפייער, פילע טראַנסמיטערז ינקאָרפּערייט שוץ קרייַז וואָס ראַדוסאַז די רעזולטאַט פון די טראַנסמיטער ווען די סוור רייזאַז. דעם מיטל אַז אַ נעבעך גלייַכן צווישן די פידער און אַנטענע וועט פירן צו אַ הויך סווער, וואָס וועט רעדוצירן די רעזולטאַט און דערפֿאַר אַ באַטייטיק אָנווער פון די טראַנסמיטטעד מאַכט.

- הויך וואָולטידזש און קראַנט לעוועלס קענען שעדיקן פידער

עס איז מעגלעך אַז די הויך וואָולטידזש און קראַנט לעוועלס געפֿירט דורך די הויך שטייענדיק כוואַליע פאַרהעלטעניש קענען אָנמאַכן שעדיקן צו אַ פידער. כאָטש אין רובֿ פאלן, די פידערז וועט זיין אַפּערייטאַד געזונט אין זייער לימאַץ און די דאַבלינג פון וואָולטידזש און קראַנט זאָל זיין אַקאַמאַדייטאַד, אָבער עס זענען עטלעכע צושטאנדן ווען שעדיקן קענען זיין געפֿירט. די קראַנט מאַקסימאַ קענען גרונט יבעריק היגע באַהיצונג וואָס קען פאַרקרימען אָדער צעלאָזן די פּלאַסטיקס געניצט, און די הויך וואָולטידזש איז באַוווסט צו גרונט אַרסינג אין עטלעכע צושטאנדן.

-דילייז געפֿירט דורך רעפלעקטיאָנס קענען פאַרשאַפן דיסטאָרשאַן:   

ווען אַ סיגנאַל איז שפיגלט דורך מיסמאַטש, עס איז שפיגלט צוריק צו די מקור, און קענען זיין שפיגלט ווידער צו די אַנטענע. 

א פאַרהאַלטן איז באַקענענ גלייַך צו צוויי מאָל די טראַנסמיסיע צייט פון די סיגנאַל צוזאמען די פידער. 

אויב דאַטן זענען טראַנסמיטטעד, דאָס קען פאַרשאַפן ינטער-סימבאָל ינטערפיראַנס, און אין אן אנדער בייַשפּיל ווו אַנאַלאָג טעלעוויזיע איז טראַנסמיטטעד, אַ "גייַסט" בילד איז געווען געזען.

ינטערעסטינגלי די אָנווער אין סיגנאַל מדרגה געפֿירט דורך אַ נעבעך VSWR איז נישט קימאַט ווי גרויס ווי עטלעכע קען ימאַדזשאַן. 

קיין סיגנאַל רעפלעקטעד דורך די מאַסע, איז שפיגלט צוריק צו די טראַנסמיטער און ווי די מאַטטשינג בייַ די טראַנסמיטער קענען געבן די סיגנאַל צו זיין שפיגלט צוריק צו די אַנטענע ווידער, די לאָססעס ינקערד זענען פאַנדאַמענטאַלי די ינטראָודוסט דורך די פידער. 

עס זענען אנדערע וויכטיק ביטן צו זיין געמאסטן אין אַנטענע עפעקטיווקייַט: די אָפּשפּיגלונג קאָואַפישאַנט, די מיסמאַטש אָנווער, און די צוריקקער אָנווער צו נאָמען אַ ביסל. VSWR איז נישט דער סוף-אַלע-זיין-אַלע פון ​​אַנטענע טעאָריע, אָבער עס איז וויכטיק.

3) VSWR vs SWR ווס PSWR ווס ISWR

די טערמינען VSWR און SWR ווערן אָפט געזען אין דער ליטעראַטור וועגן שטייענדיק כוואליעס אין רף סיסטעמען, און פילע פרעגן וועגן די חילוק.

-VSWR

די VSWR אָדער וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש אַפּלייז ספּאַסיפיקלי צו די וואָולטידזש שטייענדיק כוואליעס וואָס זענען שטעלן אַרויף אויף אַ פידער אָדער טראַנסמיסיע שורה. 

ווי עס איז גרינגער צו דעטעקט די וואָולטידזש שטייענדיק כוואליעס, און אין פילע ינסטאַנסיז וואָולטאַדזשאַז זענען מער וויכטיק אין טערמינען פון מיטל ברייקדאַון, דער טערמין VSWR איז אָפט געניצט, ספּעציעל אין רף פּלאַן געביטן.

-SWR

SWR שטייט פֿאַר שטייענדיק כוואַליע פאַרהעלטעניש. איר קענען זען עס ווי מאַטאַמאַטיקאַל אויסדרוק פון די ניט-וניפאָרמאַטי פון אַן ילעקטראָומאַגנעטיק פעלד (עם פעלד) אויף אַ טראַנסמיסיע שורה אַזאַ ווי קאָאַקסיאַל קאַבלע. 

וסואַללי, SWR איז דיפיינד ווי די פאַרהעלטעניש פון די מאַקסימום ראַדיאָ-אָפטקייַט (רף) וואָולטידזש צו די מינימום רף וואָולטידזש צוזאמען די שורה. די שטייענדיק כוואַליע פאַרהעלטעניש (SWR) האט דריי פֿעיִקייטן:

SWR האט די פאלגענדע פֿעיִקייטן:

● עס באשרייבט די וואָולטידזש און קראַנט שטייענדיק כוואליעס וואָס דערשייַנען אויף די שורה. 

● עס איז אַ דזשאַנעריק באַשרייַבונג פֿאַר קראַנט און וואָולטידזש כוואליעס. 

● עס איז אָפט געניצט אין אַסאָוסייישאַן מיט מעטער געניצט צו דיטעקט די שטייענדיק כוואַליע פאַרהעלטעניש. 

נאָטיץ: ביידע קראַנט און וואָולטידזש העכערונג און פאַלן דורך דער זעלביקער פּראָפּאָרציע פֿאַר אַ געגעבן מיסמאַטש.

א הויך SWR ינדיקייץ נעבעך טראַנסמיסיע-ליניע עפעקטיווקייַט און שפיגלט ענערגיע, וואָס קענען שעדיקן די טראַנסמיטער און פאַרמינערן טראַנסמיסיע עפעקטיווקייַט. זינט SWR יוזשאַוואַלי רעפערס צו די וואָולטידזש פאַרהעלטעניש, עס איז יוזשאַוואַלי באַוווסט ווי די וואָולטידזש וואָולטידזש פאַרהעלטעניש (VSWR).

פּסוור (מאַכט שטייענדיק וואַווע פאַרהעלטעניש):

דער טערמין מאַכט שטייענדיק כוואַליע פאַרהעלטעניש, וואָס איז אויך געוויזן עטלעכע מאָל, איז דיפיינד ווי די קוואַדראַט פון די ווסוור. אָבער, דאָס איז אַ גאַנץ פאַלאַסי ווייַל די פאָרויס און רעפלעקטעד מאַכט זענען קעסיידערדיק (אַסומינג אַז קיין פידער לאָססעס) און די מאַכט קען נישט העכערונג און פאַלן אין די זעלבע וועג ווי די וואָולטידזש און קראַנט שטייענדיק כוואַליע פאָרמס זענען די סאַמיישאַן פון ביידע פֿאָרווערטס און שפיגלט עלעמענטן.

● ISWR (קראַנט שטייענדיק וואַווע פאַרהעלטעניש):

די SWR קען אויך זיין דיפיינד ווי די פאַרהעלטעניש פון די מאַקסימום רף קראַנט צו די מינימום רף קראַנט אויף די שורה (קראַנט שטייענדיק-כוואַליע פאַרהעלטעניש אָדער יסוור). פֿאַר רובֿ פּראַקטיש צוועקן, ISWR איז די זעלבע ווי VSWR.

פֿון עטלעכע מענטשן ס פארשטאנד פון SWR און VSWR אין זייער יקערדיק פאָרעם, דאָס איז אַ גאנץ 1: 1. SWR מיטל אַז אַלע די מאַכט איר שטעלן אויף די שורה איז פּושט אויס פון די אַנטענע. אויב די SWR איז נישט 1: 1, איר שטעלן מער מאַכט ווי וואָס איז דארף און עטלעכע פון ​​די מאַכט איז שפיגלט צוריק אַראָפּ די שורה צו דיין טראַנסמיטער און דאַן אַ צונויפשטויס וואָס קען פאַרשאַפן דיין סיגנאַל איז נישט ווי ריין און קלאָר.

אָבער, וואָס איז די חילוק צווישן VSWR און SWR? SWR (שטייענדיק כוואַליע פאַרהעלטעניש) איז אַ באַגריף, הייסט די שטייענדיק כוואַליע פאַרהעלטעניש. ווסוור איז אַקשלי ווי איר מעסטן די מעאַסורעמענט דורך מעסטן די וואָולטידזש צו באַשליסן די SWR. איר קענט אויך מעסטן די SWR דורך מעסטן די קעראַנץ אָדער אפילו די מאַכט (ISWR און PSWR). אָבער פֿאַר רובֿ ינטענץ און צוועקן, ווען עמעצער זאגט SWR, זיי מיינען VSWR, אין פּראָסט שמועס זיי זענען ינטערטשיינדזשאַבאַל.

איר מיינט צו אָנכאַפּן דעם געדאַנק אַז עס איז פארבונדן צו די פאַרהעלטעניש צווישן ווי פיל מאַכט פאָרויס צו די אַנטענע ווס. ווי פיל איז ריפלעקט צוריק און אַז (אין רובֿ פאלן) די מאַכט איז פּושט צו די אַנטענע. אָבער, די סטייטמאַנץ "איר שטעלן מער מאַכט ווי וואָס איז דארף" און "דערנאָך זייַנען אַ צונויפשטויס וואָס קען פאַרשאַפן דיין סיגנאַל איז נישט ווי ריין" זענען פאַלש

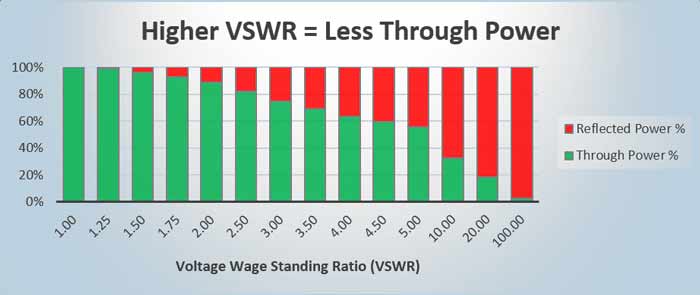
VSWR קעגן Rleflected Power

אין די קאַסעס פון העכער SWR, עטלעכע אָדער פיל פון די מאַכט איז סימפּלי ראַפלעקטאַד צו די טראַנסמיטער. עס האט גאָרנישט צו טאָן מיט אַ ריין סיגנאַל און אַלץ צו טאָן מיט פּראַטעקטינג דיין טראַנסמיטער פון ברענען און SWR איז ראַגאַרדלאַס פון די סומע פון ​​מאַכט איר פּאַמפּינג. עס סימפּלי מיטל אַז אין די אָפטקייַט, די אַנטענע סיסטעם איז נישט אַזוי עפעקטיוו ווי אַ קאַלאָריפער. דאָך, אויב איר פּרוּווט צו יבערשיקן מיט אַ אָפטקייַט, וואָלט איר בעסער וועלן אַז דיין אַנטענע זאָל האָבן די לאָואַסט SWR (יוזשאַוואַלי עפּעס ווייניקער ווי 2: 1 איז נישט אַזוי שלעכט אויף די נידעריקער באַנדס און 1.5: 1 איז גוט אין די העכער באַנדס) , אָבער פילע מולטי-באַנדע אַנטענאַז קענען זיין ביי 10: 1 אויף עטלעכע באַנדס, און איר קען געפֿינען אַז איר קענען אַרבעטן אַקסעפּטאַבלי.

4) VSWR און סיסטעם עפעקטיווקייַט
אין אַן אידעאל סיסטעם, 100% ענערגיע איז טראַנסמיטטעד פֿון די מאַכט סטאַגעס צו די מאַסע. דעם ריקווייערז אַ פּינטלעך גלייַכן צווישן די מקור ימפּידאַנס (די כאַראַקטעריסטיש ימפּידאַנס פון די טראַנסמיסיע שורה און אַלע זייַן קאַנעקטערז) און די מאַסע ימפּידאַנס. די סי וואָולטידזש פון די סיגנאַל וועט זיין די זעלבע פֿון סוף צו סוף ווייַל עס פּאַסיז אָן ינטערפיראַנס.

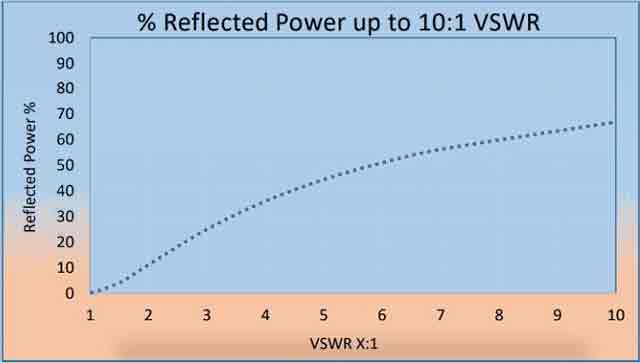
VSWR vs.% רעפלעקטעד מאַכט

אין אַ פאַקטיש סיסטעם, מיסמאַטשט ימפּידאַנסיז גרונט עטלעכע פון ​​די מאַכט צו זיין שפיגלט צוריק צו דער מקור (ווי אַ ווידערקאָל). די רעפלעקטיאָנס זייַנען קאַנסטראַקטיוו און דעסטרוקטיווע ינטערפיראַנס, וואָס פירן צו פּיקס און וואַליז אין דעם וואָולטידזש, וועריינג מיט צייט און ווייַטקייט צוזאמען די טראַנסמיסיע ליניע. ווסוור קוואַנטאַפייז די וואָולטידזש וועריאַנסיז, דערפֿאַר אן אנדער אָפט געניצט דעפֿיניציע פֿאַר וואָולטידזש שטייענדיק וואַווע פאַרהעלטעניש איז אַז דאָס איז די פאַרהעלטעניש פון דעם העכסטן וואָולטידזש צו די לאָואַסט וואָולטידזש, אין קיין פונט אויף די טראַנסמיסיע ליניע.

פֿאַר אַן אידעאל סיסטעם, וואָולטידזש קען נישט בייַטן. דעריבער, זייַן VSWR איז 1.0 (אָדער מער יוזשאַוואַלי אויסגעדריקט ווי אַ פאַרהעלטעניש פון 1: 1). ווען ריפלעקשאַנז פאַלן, וואָולטידזש פארשיידן און ווסוור איז העכער, למשל 1.2 (אָדער 1.2: 1). געוואקסן ווסוור קאָראַלייץ מיט עפעקטיווקייט פון רידוסט טראַנסמיסיע ליניע (און דעריבער קוילעלדיק טראַנסמיטער).

די עפעקטיווקייט פון טראַנסמיסיע שורות ינקריסיז דורך:
1. ינקרעאַסינג וואָולטידזש און מאַכט פאַקטאָר
2. ינקרעאַסינג וואָולטידזש און דיקריסינג מאַכט פאַקטאָר
3. דיקריסינג וואָולטידזש און מאַכט פאַקטאָר
4. דיקריסינג וואָולטידזש און ינקריסינג מאַכט פאַקטאָר

עס זענען פיר קוואַנטאַטיז וואָס דיסקרייבז די יפעקטיוונאַס פון טראַנספערינג מאַכט פון אַ שורה צו אַ מאַסע אָדער אַנטענע: די VSWR, די אָפּשפּיגלונג קאָואַפישאַנט, די מיסמאַטש אָנווער און די צוריקקער אָנווער. 

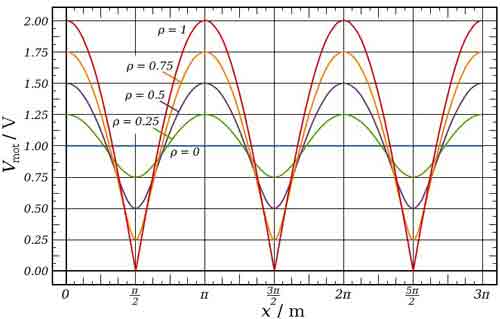
איצט, צו באַקומען אַ געפיל פֿאַר זייער טייַטש, מיר ווייַזן זיי גראַפיקלי אויף דער ווייַטער פיגור. דריי באדינגונגען: 

● די שורות פארבונדן צו אַ מאַטשט מאַסע;
● די שורות פארבונדן צו אַ קורץ מאָנאָפּאָל אַנטענע וואָס איז נישט מאַטשט (אַנטענע אַרייַנשרייַב ימפּידאַנס איז 20 - דזש 80 אָום, קאַמפּערד מיט די טראַנסמיסיע שורה ימפּידאַנס פון 50 אָום);
● די שורה איז אָופּאַנד אין די סוף ווו די אַנטענע זאָל זיין פארבונדן.

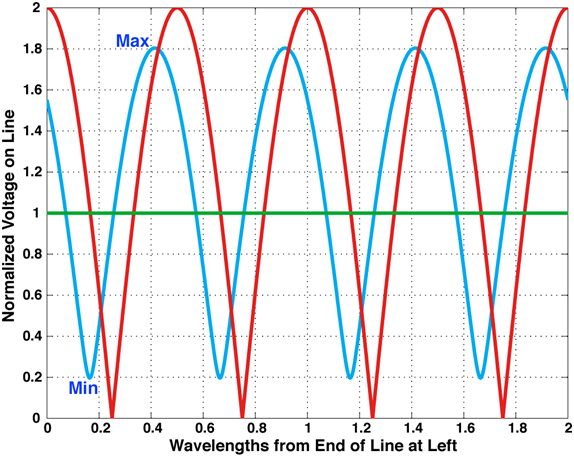
גרין ויסבייג - שטייענדיק כוואַליע אויף 50-אָום שורה מיט מאַטשט 50-אָום מאַסע אין די סוף

מיט די פּאַראַמעטערס און נומעריש ווערט ווי גייט:

פּאַראַמעטערס	נומעריקאַל ווערט
מאַסע ימפּעדאַנסע	קסנומקס אָומז
אָפּשפּיגלונג קאָואַפישאַנט	0
ווסוור	1
מיסמאַטש אָנווער	קסנומקס דב
צוריקקער אָנווער	- ∞ דב
נאָטיץ: [דאָס איז שליימעסדיק; קיין שטייענדיק כוואַליע; אַלע מאַכט גייט אין אַנטענע / מאַסע]

בלוי קורווע - שטייענדיק כוואַליע אויף 50-אָום שורה אין קורץ מאָנאָפּאָל אַנטענע

מיט די פּאַראַמעטערס און נומעריש ווערט ווי גייט:

פּאַראַמעטערס	נומעריקאַל ווערט
מאַסע ימפּעדאַנסע	20 - דזש 80 אָום
אָפּשפּיגלונג קאָואַפישאַנט	0.3805 - j0.7080
אַבסאָלוט ווערט פון אָפּשפּיגלונג קאָואַפישאַנט	0.8038
ווסוור	9.2
מיסמאַטש אָנווער	- 4.5 דב
צוריקקער אָנווער	-קסנומקס דב
נאָטיץ: [דאָס איז נישט צו גוט; מאַכט אין מאַסע אָדער אַנטענע איז אַראָפּ –4.5 דב פֿון די פאַראַנען טראַוואַלינג אַראָפּ שורה]

רויט ויסבייג - שטייענדיק כוואַליע אויף שורה מיט עפענען קרייַז ביי לינקס סוף (אַנטענע טערמינאַלס)

מיט די פּאַראַמעטערס און נומעריש ווערט ווי גייט:

פּאַראַמעטערס	נומעריקאַל ווערט
מאַסע ימפּעדאַנסע	∞
אָפּשפּיגלונג קאָואַפישאַנט	1
ווסוור	∞
מיסמאַטש אָנווער	- 0 דב
צוריקקער אָנווער	קסנומקס דב
נאָטיץ: [דאָס איז זייער שלעכט: קיין מאַכט טראַנספערד איבער די סוף פון די שורה]

▲צוריק▲

3. וויכטיק פּאַראַמעטער ינדאַקייטערז פון SWR

1) טראַנסמיסיע שורות און SWR

קיין אָנפירער וואָס פירן אַן אַק קראַנט קענען זיין באהאנדלט ווי אַ טראַנסמיסיע שורה, אַזאַ ווי די אָוווערכעד דזשייאַנץ וואָס פאַרשפּרייטן די מאַכט מאַכט איבער די לאַנדשאַפט. ינקאָרפּערייטינג אַלע די פאַרשידענע פארמען פון טראַנסמיסיע שורות וואָלט פאַלן באטייטיק אַרויס דעם פאַרנעם פון דעם אַרטיקל. און פּאַראַלעל-אָנפירער (אַקאַ, עפענען-דראָט, פֿענצטער שורה, לייטער ליניע, אָדער צווילינג-פירן ווי מיר וועט רופן עס) ווי געוויזן אין פיגורע 1.

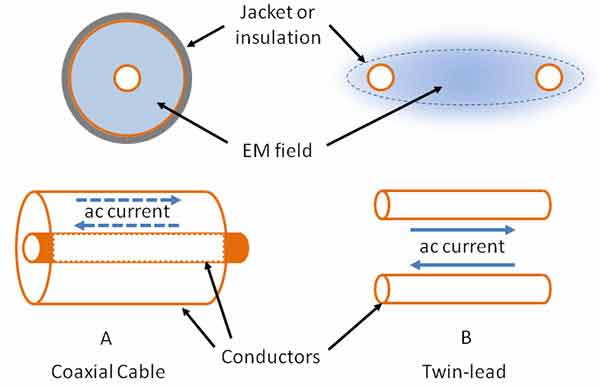
דערקלערונג: קאָאַקסיאַל קאַבלע (A) באשטייט פון אַ האַרט אָדער סטראַנדיד צענטער אָנפירער סעראַונדאַד דורך אַ ינסאַלייטינג פּלאַסטיק אָדער לופט דיעלעקטריק און אַ טובולאַר שילד וואָס איז אָדער האַרט אָדער וואָווען דראָט צאָפּ. א פּלאַסטיק רעקל סעראַונדז די שילד צו באַשיצן די קאָנדוקטאָרס. צווילינג-פירן (B) באשטייט פון אַ פּאָר פון פּאַראַלעל האַרט אָדער סטראַנדיד ווירעס. די ווירעס זענען געהאלטן אין פּלאַץ דורך מאָולדיד פּלאַסטיק (פֿענצטער שורה, צווילינג-פירן) אָדער דורך סעראַמיק אָדער פּלאַסטיק ינסאַלייטערז (לייטער שורה).

דער שטראָם פלאָוז צוזאמען די ייבערפלאַך פון די קאַנדאַקטערז (זען די סיידבאַר אויף "הויט ווירקונג") אין פאַרקערט אינסטרוקציעס. סאַפּרייזינגלי, די רף ענערגיע פלאָוינג צוזאמען די שורה טוט נישט טאַקע לויפן אין די קאָנדוקטאָרס ווו די קראַנט איז. עס טראַוואַלז ווי אַ ילעקטראָומאַגנעטיק כוואַליע (EM) אין די פּלאַץ צווישן און אַרום די קאַנדאַקטערז. 

פיגורע 1 ינדיקייץ ווו די פעלד איז ליגן אין ביידע קאָאַקס און צווילינג פירן. פֿאַר קאָאַקס, די פעלד איז גאָר קאַנטיינד אין די דיעלעקטריק צווישן די אָנפירער און שילד. פֿאַר צווילינג-פירן, די פעלד איז אָבער די מערסט שטאַרק אַרום און צווישן די קאַנדאַקטערז, אָבער אָן אַ אַרומיק שילד, עטלעכע פון ​​די פעלד יקסטענדז אין די פּלאַץ אַרום די שורה.

דאָס איז וואָס קאָאַקס איז אַזוי פאָלקס - עס קען נישט לאָזן די סיגנאַלז ינטעראַקשאַן מיט סיגנאַלז און קאָנדוקטאָרס אַרויס די שורה. צווילינג-פירן, אויף די אנדערע האַנט, דאַרף זיין געזונט אַוועק (עטלעכע ליניע ברייט איז גענוג) פון אנדערע קאָרמען שורות און קיין מעטאַל ייבערפלאַך. פארוואס נוצן צווילינג-פירן? עס בכלל האט נידעריקער לאָססעס ווי קאָאַקס, אַזוי עס איז אַ בעסער ברירה ווען סיגנאַל אָנווער איז אַ וויכטיק באַטראַכטונג.

טראַנסמיסיע ליניע טוטאָריאַל פֿאַר ביגינערז (מאָקער: AT&T)

וואָס איז הויט ווירקונג?

אויבן וועגן 1 כז, די AC קעראַנץ לויפן אין אַ ינקריסינגלי דין שיכטע צוזאמען די ייבערפלאַך פון קאַנדאַקטערז. דאָס איז די הויט ווירקונג. עס אַקערז ווייַל עדי קעראַנץ ין דער אָנפירער מאַגנעטיק פעלדער וואָס שטופּן קראַנט צו די ויסווייניקסט ייבערפלאַך פון די אָנפירער. אין 1 מהז אין קופּער, רובֿ קראַנט איז ריסטריקטיד צו די ויסווייניקסט 0.1 מם פון די אָנפירער, און דורך 1 גהז, די קראַנט איז סקוויזד אין אַ שיכטע פון ​​בלויז µm דיק.

2) רעפלעקטיאָן און טראַנסמיסיע קאָואַפישאַנץ

אָפּשפּיגלונג קאָואַפישאַנט איז די בראָכצאָל פון אַן אינצידענט סיגנאַל שפיגלט צוריק פֿון אַ מיסמאַטש. דער אָפּשפּיגלונג קאָואַפישאַנט איז אויסגעדריקט ווי ρ אָדער Γ, אָבער די סימבאָלס קענען אויך זיין געניצט צו פאָרשטעלן VSWR. עס איז גלייַך פארבונדן צו די VSWR דורך

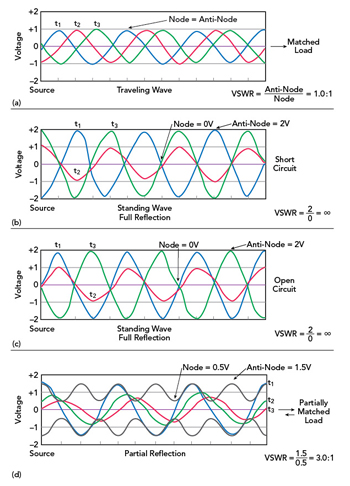
 | Γ | = (VSWR - 1) / (VSWR + 1) (A)

פיגורע. דאָס איז די בראָכצאָל פון אַ סיגנאַל רעפלעקטעד דורך די מאַסע ימפּידאַנס און יז איז אויסגעדריקט ווי אַ פּראָצענט.

פֿאַר אַ שליימעסדיק גלייַכן, קיין סיגנאַל איז שפיגלט דורך די מאַסע (דאָס איז טאָוטאַלי אַבזאָרבד), אַזוי די אָפּשפּיגלונג קאָואַפישאַנט איז נול. 

פֿאַר אַ עפענען אָדער קורץ קרייַז, די גאנצע סיגנאַל איז שפיגלט צוריק, אַזוי די אָפּשפּיגלונג קאָואַפישאַנט איז אין ביידע פאלן 1. באַמערקונג אַז די דיסקוסיע דילז בלויז מיט די גרייס פון דער אָפּשפּיגלונג קאָואַפישאַנט.  

Γ האט אויך אַ פארבונדן פאַסע ווינקל, וואָס דיסטינגגווישיז צווישן אַ קורץ קרייַז און אַ עפענען קרייַז, ווי געזונט ווי אַלע שטאַטן אין צווישן. 

פֿאַר בייַשפּיל, אָפּשפּיגלונג פון אַ עפענען קרייַז רעזולטאַטן אין אַ 0 גראַד פאַסע ווינקל צווישן די אינצידענט און שפיגלט כוואַליע, וואָס מיטל אַז די רעפלעקטעד סיגנאַל מוסיף אין פאַסע מיט די ינקאַמינג סיגנאַל אין די עפענען קרייַז אָרט; דאס הייסט די אַמפּליטוד פון די שטייענדיק כוואַליע איז טאָפּל ווי די ינקאַמינג כוואַליע. 

אין קאַנטראַסט, אַ קורץ קרייַז ריזאַלטיד אין אַ 180 גראַד פאַסע ווינקל צווישן די אינצידענט און שפיגלט סיגנאַל, וואָס מיטל אַז דער שפיגלט סיגנאַל איז פאַרקערט אין פאַסע צו די ינקאַמינג סיגנאַל, אַזוי זייער אַמפּליטודז אַראָפּרעכענען, ריזאַלטינג אין נול. דאָס קען זיין געוויזן אין פיגורעס 1 אַ און ב.

וווּ דער אָפּשפּיגלונג קאָואַפישאַנט איז די בראָכצאָל פון אַ ינסידענט סיגנאַל רעפלעקטעד צוריק פון אַ ימפּידאַנס מיסמאַטש אין אַ קרייַז אָדער טראַנסמיסיע שורה, די טראַנסמיסיע קאָואַפישאַנט איז די בראָכצאָל פון די ינסידענט סיגנאַל וואָס איז דערשייַנען אין דער רעזולטאַט. 

עס איז אַ פֿונקציע פון ​​דער סיגנאַל וואָס איז שפיגלט ווי געזונט ווי ינערלעך קרייַז ינטעראַקשאַנז. עס אויך האט אַ קאָראַספּאַנדינג אַמפּליטוד און פאַסע.

3) וואָס איז צוריק לאָס און ינסערשאַן לאָס?

צוריקקער אָנווער איז די פאַרהעלטעניש פון די מאַכט מדרגה פון די רעפלעקטעד סיגנאַל צו די מאַכט מדרגה פון די ינפּוט סיגנאַל אויסגעדריקט אין דעסיבאַלז (דב), י.ע.

RL (dB) = 10 log10 Pi / Pr (B)

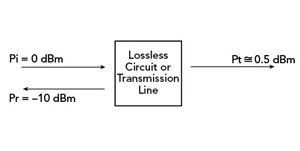
פיגורע 2. ווייַזן אָנווער און ינסערשאַן אָנווער אין אַ לאָססלעסס קרייַז אָדער טראַנסמיסיע שורה.

אין פיגורע 2, אַ 0-דבם סיגנאַל, פּי, איז געווענדט צו דער טראַנסמיסיע ליניע. די רעפלעקטעד מאַכט, פּר, איז געוויזן ווי -10 דבם און די צוריקקער אָנווער איז 10 דב. די העכער די ווערט, די בעסער די גלייַכן, וואָס איז, פֿאַר אַ שליימעסדיק גלייַכן, די צוריקקער אָנווער, ידעאַללי, איז ∞, אָבער אַ צוריקקער אָנווער פון 35 צו 45 דב, איז יוזשאַוואַלי געהאלטן אַ גוט גלייַכן. סימילאַרלי, פֿאַר אַ עפענען קרייַז אָדער אַ קורץ קרייַז, די ינסידענט מאַכט איז שפיגלט צוריק. דער צוריקקער אָנווער פֿאַר די קאַסעס איז 0 דב.

ינסערשאַן אָנווער איז די פאַרהעלטעניש פון די מאַכט מדרגה פון די טראַנסמיטטעד סיגנאַל צו די מאַכט מדרגה פון די ינפּוט סיגנאַל אויסגעדריקט אין דעסיבאַלז (דב), הייסט

IL (dB) = 10 log10 Pi / Pt (C)

פּי = פּט + פּר; פּט / פּי + פּר / פּי = 1                                                                            

ריפערינג צו פיגורע 2, פּר פון -10 דבם מיטל אַז 10 פּראָצענט פון די ינסידענט מאַכט איז שפיגלט. אויב די קרייַז אָדער טראַנסמיסיע שורה איז לאָססלעסס, 90 פּראָצענט פון די ינסידענט מאַכט איז טראַנסמיטטעד. די ינסערשאַן אָנווער איז דעריבער בעערעך 0.5 דב, ריזאַלטינג אין אַ טראַנסמיטטעד מאַכט פון -0.5 דבם. אויב עס זענען ינערלעך לאָססעס, די ינסערשאַן אָנווער וואָלט זיין גרעסער.

4) וואָס איז S- פּאַראַמעטערס?

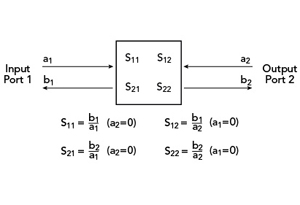פיגורע. S- פּאַראַמעטער פאַרטרעטונג פון אַ צוויי-פּאָרט מייקראַווייוו קרייַז.

ניצן S- פּאַראַמעטערס, די RF פאָרשטעלונג פון אַ קרייַז קענען זיין גאָר קעראַקטערייזד אָן די נויט צו וויסן די ינערלעך זאַץ. פֿאַר די צוועקן, די קרייַז איז אָפט ריפערד צו ווי אַ "שוואַרץ קעסטל." ינערלעך קאַמפּאָונאַנץ קענען זיין אַקטיוו (י.ע., אַמפּלאַפייערז) ​​אָדער פּאַסיוו. דער בלויז סטיפּיאַליישאַן איז אַז די S- פּאַראַמעטערס זענען באשלאסן פֿאַר אַלע פריקוואַנסיז און באדינגונגען (למשל טעמפּעראַטור, אַמפּלאַפייער פאָרורטייל) פון אינטערעס און אַז די קרייַז איז לינעאַר (ד"ה, די פּראָדוקציע איז גלייַך פּראַפּאָרשאַנאַל צו זיין אַרייַנשרייַב). פיגורע 3 איז אַ פאַרטרעטונג פון אַ פּשוט מייקראַווייוו קרייַז מיט איין ינפּוט און איין רעזולטאַט (גערופֿן פּאָרץ). יעדער פּאָרט האט אַן אינצידענט סיגנאַל (אַ) און אַ רעפלעקטעד סיגנאַל (ב). דורך וויסן די S- פּאַראַמעטערס (ד"ה S11, S21, S12, S22) פון דעם קרייַז, איר קענען באַשליסן די ווירקונג אויף קיין סיסטעם אין וואָס עס איז אינסטאַלירן.

ס-פּאַראַמעטערס זענען באשלאסן דורך מעזשערמאַנט אונטער קאַנטראָולד טנאָים. ניצן אַ ספּעציעל שטיק פון פּרובירן ויסריכט גערופֿן אַ נעץ אַנאַליזער, אַ סיגנאַל (אַ 1) איז ינפּוט אין פּאָרט 1 מיט פּאָרט 2 טערמאַנייטיד אין אַ סיסטעם מיט אַ קאַנטראָולד ימפּידאַנס (טיפּיקלי 50 אָום). דער אַנאַליזער מעסטן און רעקאָרדירט ​​סיימאַלטייניאַסלי a1, b1 און b2 (a2 = 0). דער פּראָצעס איז דעמאָלט ריווערסט, ד"ה מיט אַ סיגנאַל (a2) ינפּוט צו פּאָרט 2, די אַנאַליזער מעסטן a2, b2 און b1 (a1 = 0). אין זיין סימפּלאַסט פאָרעם, די נעץ אַנאַליזער בלויז מעסטן די אַמפּליטודעס פון די סיגנאַלז. דאָס איז גערופֿן אַ סקאַלאַר נעץ אַנאַליזער און איז גענוג פֿאַר דיטערמאַנינג קוואַנטאַטיז אַזאַ ווי VSWR, RL און IL. פֿאַר גאַנץ קרייַז כאַראַקטעריזיישאַן, אָבער, די פאַסע איז אויך דארף און ריקווייערז די נוצן פון אַ וועקטאָר נעץ אַנאַליזער. די S- פּאַראַמעטערס זענען באשלאסן דורך די פאלגענדע שייכות:

ס 11 = ב 1 / אַ 1; ס 21 = ב 2 / אַ 1; S22 = b2 / a2; S12 = b1 / a2 (D)

S11 און S22 זענען ריספּעקטיוו קאָואַפישאַנץ פון די אַרייַנשרייַב און רעזולטאַט פּאָרט אָפּשפּיגלונג קאָואַפישאַנץ; בשעת S21 און S12 זענען די פאָרווערדינג און פאַרקערט טראַנסמיסיע קאָואַפישאַנץ פון די קרייַז. RL איז פארבונדן צו די אָפּשפּיגלונג קאָואַפישאַנץ דורך די שייכות

RLPort 1 (dB) = -20 log10 | S11 | און רלפּאָרט 2 (דב) = -20 לאָג10 | S22 | (E)

IL איז פארבונדן מיט די ריליישאַנשיפּ טראַנסמיסיע קאָואַפישאַנץ

IL פון פּאָרט 1 צו פּאָרט 2 (dB) = -20 log10 | S21 | און פון Port 2 to Port 1 (dB) = -20 log10 | S12 | (F)

די פאַרטרעטונג קענען זיין עקסטענדעד צו מייקראַווייוו סערקאַץ מיט אַ אַרביטראַריש נומער פון פּאָרץ. די נומער פון S- פּאַראַמעטערס גייט אַרויף דורך די קוואדראט פון די נומער פון פּאָרץ, אַזוי די מאטעמאטיק ווערט מער ינוואַלווד, אָבער איז מאַנידזשאַבאַל מיט מאַטריץ אַלגעבראַ.

5) וואָס איז ימפּעדאַנס-מאַטטשינג?

ימפּידאַנסע איז אָפּאָזיציע פון ​​עלעקטריקאַל ענערגיע ווען עס מאָוועס אַוועק פון זיין מקור.  

סינטשראָניזינג מאַסע און מקור ימפּידאַנס וועט באָטל מאַכן די ווירקונג לידינג צו מאַקסימום מאַכט אַריבערפירן. 

דעם איז באַוווסט ווי די מאַקסימום מאַכט אַריבערפירן טעאָרעם: מאַקסימום מאַכט אַריבערפירן טעאָרעם איז קריטיש אין ראַדיאָפרעקווענסי טראַנסמיסיע אַסעמבליז, און אין באַזונדער, אין די שטעלן זיך פון רף אַנטענאַז.

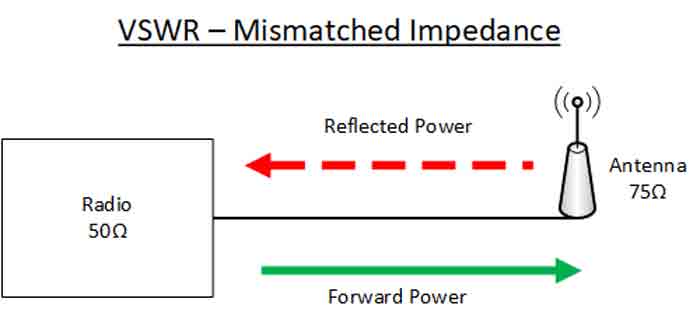
ימפּעדאַנס מאַטטשינג איז קריטיש פֿאַר די עפעקטיוו פאַנגקשאַנינג פון רף סעטאַפּס ווו איר ווילן צו מאַך וואָולטידזש און מאַכט אָפּטימאַללי. אין רף פּלאַן, די ריכטן פון מקור און מאַסע ימפּידאַנסיז מאַקסאַמייז די טראַנסמיסיע פון ​​רף מאַכט. אַנטענאַז וועט באַקומען מאַקסימום אָדער אָפּטימאַל מאַכט אַריבערפירן וווּ זייער ימפּידאַנס איז מאַטשט צו די רעזולטאַט ימפּידאַנס פון די טראַנסמיסיע מקור.

50 אָום ימפּידאַנס איז דער נאָרמאַל פֿאַר דיזיינינג רובֿ רף סיסטעמען און קאַמפּאָונאַנץ. קאָאַקסיאַל קאַבלע וואָס דיפּענדינג אויף די קאַנעקטיוויטי אין אַ נומער פון רף אַפּלאַקיישאַנז האט אַ טיפּיש ימפּידאַנס פון 50 אָום. אין די 1920 ס געפֿונען רף פאָרשונג אַז די אָפּטימאַל ימפּידאַנס פֿאַר די אַריבערפירן פון רף סיגנאַלז וואָלט זיין צווישן 30 און 60 Ohm דיפּענדינג אויף וואָולטידזש און מאַכט אַריבערפירן. מיט לעפיערעך סטאַנדערדייזד ימפּידאַנס אַלאַוז די ריכטן צווישן קאַבלינג און קאַמפּאָונאַנץ אַזאַ ווי וויפי אָדער בלועטאָאָטה אַנטענאַז. פּקבס און אַטטענואַטאָרס. א נומער פון שליסל אַנטענע טייפּס האָבן אַ ימפּידאַנס פון 50 אָום, אַרייַנגערעכנט ZigBee GSM GPS און LoRa

אָפּשפּיגלונג קאָואַפישאַנט - מקור: וויקיפּעדיע

א מיסמאַטש אין ימפּידאַנס פירט צו וואָולטידזש און קראַנט רעפלעקטיאָנס, און אין רף סעטאַפּס דעם מיטל אַז סיגנאַל מאַכט וועט זיין שפיגלט צוריק צו זיין מקור, די פּראָפּאָרציע איז לויט די גראַד פון מיסמאַטש. דעם קענען זיין קעראַקטערייזד ניצן ווסוור וואָולטידזש שטייענדיק וואַווע פאַרהעלטעניש (VSWR), וואָס איז אַ מאָס פון די עפעקטיווקייט פון אַריבערפירן פון רף מאַכט פֿון זיין מקור צו אַ מאַסע, אַזאַ ווי אַן אַנטענע.

מיסמאַטשינג צווישן מקור און מאַסע ימפּידאַנסיז, פֿאַר בייַשפּיל אַ 75 אָום אַנטענע און 50 אָום קאָאַקס קאַבלינג, קענען זיין באַקומען מיט אַ פאַרשיידנקייַט פון ימפּידאַנס ריכטן דעוויסעס אַזאַ ווי רעסיסטאָרס אין סעריע, טראַנספאָרמערס, ייבערפלאַך מאָונטעד ימפּידאַנס ריכטן פּאַדס אָדער אַנטענע טונערס.

אין עלעקטראָניק, ימפּידאַנס ריכטן ינוואַלווז קריייטינג אָדער אָלטערנייטינג אַ קרייַז אָדער עלעקטראָניש אַפּלאַקיישאַן אָדער קאָמפּאָנענט, אַזוי אַז די ימפּידאַנס פון די עלעקטריקאַל מאַסע גלייַכן די ימפּידאַנס פון די מאַכט אָדער דרייווינג מקור. דער קרייַז איז ענדזשאַנירד אָדער גירד אַזוי אַז די ימפּידאַנסיז דערשייַנען די זעלבע.

ווען איר זוכט אין סיסטעמען וואָס אַרייַננעמען טראַנסמיסיע שורות, עס איז נייטיק צו פֿאַרשטיין אַז מקורים, טראַנסמיסיע שורות / פידערז און לאָודז אַלע האָבן אַ כאַראַקטעריסטיש ימפּידאַנס. 50Ω איז אַ זייער פּראָסט סטאַנדאַרט פֿאַר רף אַפּלאַקיישאַנז, כאָטש אנדערע ימפּידאַנסאַז קען טייל מאָל זיין געוויזן אין עטלעכע סיסטעמען.

כּדי צו באַקומען די מאַקסימום מאַכט אַריבערפירן פון די מקור צו די טראַנסמיסיע שורה, אָדער די טראַנסמיסיע שורה צו די מאַסע, צי עס איז אַ רעסיסטאָר, אַ אַרייַנשרייַב צו אן אנדער סיסטעם אָדער אַן אַנטענע, די ימפּידאַנס לעוועלס מוזן גלייַכן.

אין אנדערע ווערטער פֿאַר אַ 50Ω סיסטעם, די מקור אָדער סיגנאַל גענעראַטאָר מוזן האָבן אַ מקור ימפּידאַנס פון 50Ω, די טראַנסמיסיע שורה מוזן זיין 50Ω און אַזוי די מאַסע.

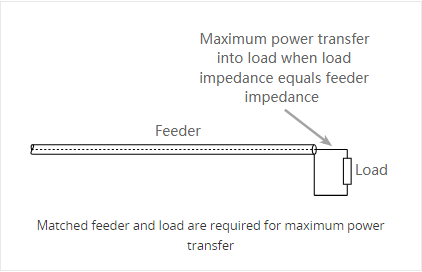
ישוז ווען מאַכט איז טראַנספערד אין די טראַנסמיסיע שורה אָדער פידער און עס טראַוואַלז צו די מאַסע. אויב עס איז אַ מיסמאַטש, דאָס הייסט, די מאַסע ימפּידאַנס איז נישט גלייך צו דער פון די טראַנסמיסיע שורה, עס איז ניט מעגלעך צו אַריבערפירן אַלע די מאַכט.

ווי מאַכט קען נישט פאַרשווינדן, די מאַכט וואָס איז נישט טראַנספערד אין די מאַסע מוזן גיין ערגעץ און דאָרט עס טראַוואַלז צוריק צוזאמען די טראַנסמיסיע שורה צוריק צו דער מקור.

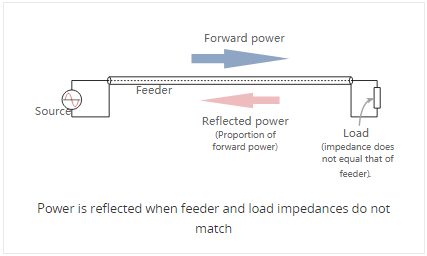
ווען דאָס כאַפּאַנז, די וואָולטידזש און קעראַנץ פון די פאָרויס און שפיגלט כוואליעס אין די פידער לייגן אָדער אַראָפּרעכענען ביי פאַרשידענע פונקטן צוזאמען די פידער לויט די פייזאַז. אין דעם וועג שטייענדיק כוואליעס זענען שטעלן זיך.

די וועג פון די ווירקונג אַקערז קענען זיין דעמאַנסטרייטיד מיט אַ לענג פון שטריק. אויב איינער עק איז לינקס פריי און די אנדערע איז אריבערגעפארן אַרויף אַ אַראָפּ, די כוואַליע באַוועגונג קענען זיין קענטיק צו רירן אַראָפּ צוזאמען די שטריק. אָבער אויב איינער סוף איז פאַרפעסטיקט, אַ שטייענדיק כוואַליע באַוועגונג איז שטעלן זיך, און די פונקטן פון מינימום און מאַקסימום ווייבריישאַן קענען זיין געוויזן.

די מאַסע קעגנשטעל איז נידעריקער ווי די פידער ימפּידאַנס וואָולטידזש און קראַנט מאַגנאַטודז זענען שטעלן זיך. דאָ די גאַנץ קראַנט ביי די מאַסע פונט איז העכער ווי די פון די בישליימעס מאַטשט שורה, כוועראַז די וואָולטידזש איז ווייניקער.

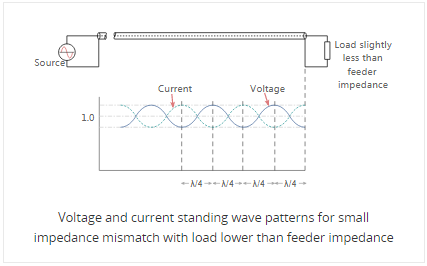
די וואַלועס פון קראַנט און וואָולטידזש צוזאמען די פידער בייַטן צוזאמען די פידער. פֿאַר קליין וואַלועס פון שפיגלט מאַכט די וואַוועפאָרם איז כּמעט סינוסוידאַל, אָבער פֿאַר גרעסערע וואַלועס עס ווערט מער ווי אַ פול-כוואַליע רעקטאַפייד סינוס כוואַליע. דעם וואַוועפאָרם באשטייט פון וואָולטידזש און קראַנט פון די פאָרויס מאַכט פּלוס וואָולטידזש און קראַנט פון די שפיגלט מאַכט.

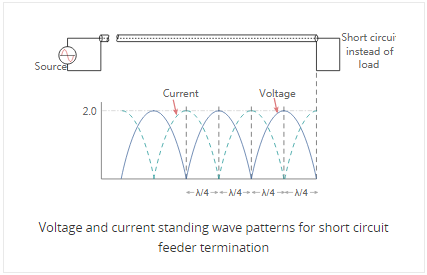
אין אַ ווייַטקייט אַ פערטל פון אַ ווייוולענגט פון די מאַסע די קאַמביינד וואָולטידזש דערגרייכן אַ מאַקסימום ווערט בשעת די קראַנט איז מינימום. אין אַ ווייַטקייט האַלב אַ ווייוולענגט פון די מאַסע די וואָולטידזש און קראַנט זענען די זעלבע ווי ביי די מאַסע.

א ענלעך סיטואַציע אַקערז ווען די מאַסע קעגנשטעל איז גרעסער ווי די פידער ימפּידאַנס, אָבער דאָס מאָל די גאַנץ וואָולטידזש ביי די מאַסע איז העכער ווי די ווערט פון די בישליימעס מאַטשט שורה. די וואָולטידזש ריטשאַז אַ מינימום אין אַ ווייַטקייט 1/4 פון אַ ווייוולענגט פון דער מאַסע און די קראַנט איז מאַקסימום. אין אַ ווייַטקייט פון אַ האַלב ווייוולענגט פון דער מאַסע, די וואָולטידזש און קראַנט זענען די זעלבע ווי ביי די מאַסע.

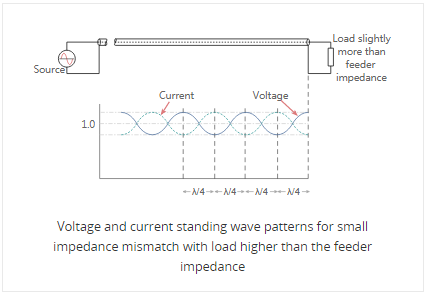
ווען עס איז אַ עפן קרייַז געשטעלט אין די סוף פון די שורה, די שטייענדיק כוואַליע מוסטער פֿאַר די פידער איז ענלעך צו דער פון די קורץ קרייַז, אָבער מיט די וואָולטידזש און קראַנט פּאַטערנז פאַרקערט.

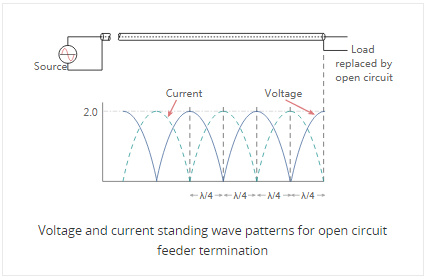
▲צוריק▲

6) וואָס איז רעפלעקטעד ענערגיע?
ווען אַ טראַנסמיטטעד כוואַליע שלאָגן אַ גרענעץ אַזאַ ווי די צווישן די לאָססלעסס טראַנסמיסיע שורה און מאַסע (זען פיגורע 1. ווייטער), עטלעכע ענערגיע וועט זיין טראַנסמיטטעד צו די מאַסע און עטלעכע וועט זיין שפיגלט. די אָפּשפּיגלונג קאָואַפישאַנט דערציילט די ינקאַמינג און שפיגלט כוואליעס ווי:

Γ = V- / V + (עקוו. 1)

וואו V- איז די שפיגלט כוואַליע און V + איז די ינקאַמינג כוואַליע. VSWR איז שייך צו די גרייס פון דעם וואָולטידזש אָפּשפּיגלונג קאָואַפישאַנט (Γ) דורך:

VSWR = (1 + | Γ |) / (1 - | Γ |) (Eq. 2)

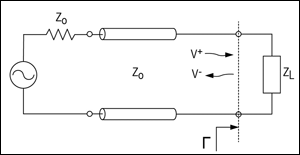
VSWR קענען ווערן געמאסטן גלייך מיט אַ SWR מעטער. אַ רף פּרובירן קיילע אַזאַ ווי אַ וועקטאָר נעץ אַנאַליזער (וונאַ) קענען ווערן גענוצט צו מעסטן די אָפּשפּיגלונג קאָואַפישאַנץ פון די אַרייַנשרייַב פּאָרט (S11) און די רעזולטאַט פּאָרט (S22). S11 און S22 זענען עקוויוואַלענט צו Γ ביי די אַרייַנשרייַב און רעזולטאַט פּאָרט. די וונאַ ס מיט מאַט מאָדעס קענען אויך גלייַך רעכענען און אַרויסווייַזן די ריזאַלטינג VSWR ווערט.

דער צוריקקער אָנווער ביי די אַרייַנשרייַב און רעזולטאַט פּאָרץ קענען זיין קאַלקיאַלייטיד דורך די אָפּשפּיגלונג קאָואַפישאַנט, S11 אָדער S22, ווי גייט:

רלין = 20 לאָג 10 | ס 11 | דב (עק. 3)

RLOUT = 20log10 | S22 | דב (עק 4)

די אָפּשפּיגלונג קאָואַפישאַנט איז קאַלקיאַלייטיד דורך די כאַראַקטעריסטיש ימפּידאַנס פון די טראַנסמיסיע שורה און די מאַסע ימפּידאַנס ווי גייט:

Γ = (ZL - ZO) / (ZL ​​+ ZO) (עק 5)

וווּ ZL איז די מאַסע ימפּידאַנס און ZO איז די כאַראַקטעריסטיש ימפּידאַנס פון די טראַנסמיסיע שורה (פיגורע 1).

VSWR קענען אויך זיין אויסגעדריקט אין טערמינען פון זל און זאָ. סאַבסטיטוטינג יקווייזשאַן 5 אין יקווייזשאַן 2, מיר באַקומען:

VSWR = [1 + | (ZL - ZO) / (ZL ​​+ ZO) |] / [1 - | (ZL - ZO) / (ZL ​​+ ZO) |] = (ZL + ZO + | ZL - ZO |) / (ZL + ZO - | ZL - ZO |)

פֿאַר ZL> ZO, | ZL - ZO | = זל - זאָ

דעריבער:

VSWR = (ZL + ZO + ZL - ZO) / (ZL ​​+ ZO - ZL + ZO) = ZL / ZO. (עק 6)
פֿאַר ZL <ZO, | ZL - ZO | = זאָ - זל

דעריבער:

VSWR = (ZL + ZO + ZO - ZL) / (ZL ​​+ ZO - ZO + ZL) = ZO / ZL. (עק 7)

מיר האָבן שוין אנגעוויזן אַז VSWR איז אַ ספּעסיפיקאַטיאָן געגעבן אין פאַרהעלטעניש פאָרעם קאָרעוו צו 1, ווי אַ ביישפּיל 1.5: 1. עס זענען צוויי ספּעציעל קאַסעס פון VSWR, ∞: 1 און 1: 1. ינפיניטי צו איינער אַקערז ווען די מאַסע איז אַן אָפֿן קרייַז. 1: 1 פאַרהעלטעניש ווען די מאַסע איז בישליימעס גלייַכן צו די כאַראַקטעריסטיש ימפּידאַנס פון די טראַנסמיסיע שורה.

VSWR איז דיפיינד פֿון די שטייענדיק כוואַליע אַז ערייזאַז אויף די טראַנסמיסיע שורה זיך דורך:

VSWR = | VMAX | / | VMIN | (עק 8)

וווּ VMAX איז די מאַקסימום אַמפּליטוד און VMIN די מינימום אַמפּליטוד פון שטייענדיק כוואַליע. מיט צוויי סופּער ימפּאָוזד כוואליעס, די מאַקסימום אַקערז מיט קאַנסטראַקטיוו ינטערפיראַנס צווישן די ינקאַמינג און שפיגלט כוואליעס. אזוי:

VMAX = V + + V- (עק. 9)

פֿאַר מאַקסימום קאַנסטראַקטיוו ינטערפיראַנס. די מינימום אַמפּליטוד אַקערז מיט דיקאַנסטראַקטיוו ינטערפיראַנס, אָדער:

VMIN = V + - V- (עק 10)

סובסטיטוטיאָן יקווייזשאַנז 9 און 10 אין די יקווייזשאַן 8 ייעלדס


VSWR = | VMAX | / | VMIN | = (V + + V -) / (V + - V-) (עק. 11)

פאַרבייַטן יקווייזשאַן 1 אין יקווייזשאַן 11, מיר באַקומען:

VSWR = V + (1 + | Γ |) / (V + (1 - | Γ |) = (1 + | Γ |) / (1 - | Γ |) (Ekv. 12)

עקוואַטיאָן 12 איז יקווייזשאַן 2 סטייטיד אין די אָנהייב פון דעם אַרטיקל.

▲צוריק▲

4. VSWR קאַלקולאַטאָר: ווי צו רעכענען VSWR? 

ימפּידאַנס מיסמאַטשאַז רעזולטאַט אין שטייענדיק כוואליעס צוזאמען די טראַנסמיסיע ליניע, און SWR איז דיפיינד ווי די פאַרהעלטעניש פון די אַמפּליטוד פון די שטייענדיק כוואַליע אין אַן אַנטינאָדע (מאַקסימום) צו די אַמפּליטוד אין אַ נאָדע (מינימום) צוזאמען די שורה.

די ריזאַלטינג פאַרהעלטעניש איז נאָרמאַלי אויסגעדריקט ווי אַ פאַרהעלטעניש, ע.ג.

אין פיר, עס איז אַ אָנווער אויף קיין פידערז אָדער טראַנסמיסיע ליניע. צו מעסטן די VSWR, פאָרווערד און פאַרקערט מאַכט איז דיטעקטאַד אין דעם פונט אין די סיסטעם, און דאָס איז קאָנווערטעד צו אַ VSWR פיגור. 

אויף דעם וועג, די VSWR איז געמאסטן אין אַ באַזונדער פונט און די וואָולטידזש מאַקסימאַ און מינימאַ טאָן ניט דאַרפֿן צו זיין באשלאסן אין די לענג פון די שורה.

די וואָולטידזש קאָמפּאָנענט פון אַ שטייענדיק כוואַליע אין אַ יונאַפאָרמלי טראַנסמיסיע שורה באשטייט פון די פאָרווערד כוואַליע (מיט אַמפּליטוד ווף) סופּערפּאָוזד אויף דער שפיגלט כוואַליע (מיט אַמפּליטוד וור). רעפלעקטיאָנס פאַלן ווי אַ רעזולטאַט פון דיסקאָנטינויטיעס, אַזאַ ווי אַ ימפּערפעקשאַן אין אַן אַנדערש מונדיר טראַנסמיסיע שורה, אָדער ווען אַ טראַנסמיסיע ליניע איז טערמאַנייטיד מיט אנדערע ווי זייַן קוואַליטעט ימפּידאַנס.

אויב איר זענט אינטערעסירט אין דיטערמאַנינג די פאָרשטעלונג פון אַנטענאַז, די VSWR זאָל שטענדיק זיין געמאסטן ביי די אַנטענע טערמינאַלס זיך ווי אין די רעזולטאַט פון די טראַנסמיטער. צוליב אָהמיק לאָססעס אין די טראַנסמיטט קאַבלינג, עס וועט זיין באשאפן אַן אילוזיע צו האָבן אַ בעסער אַנטענע VSWR, אָבער דאָס איז בלויז ווייַל די לאָססעס דאַמפּ די פּראַל פון אַ פּלוצעמדיק אָפּשפּיגלונג אין די אַנטענע טערמינאַלס.

זינט די אַנטענע איז יוזשאַוואַלי לאָוקייטאַד עטלעכע ווייַטקייט פון די טראַנסמיטער, עס דאַרף אַ פיטער שורה צו אַריבערפירן מאַכט צווישן די צוויי. אויב די קאָרמען ליניע האט קיין אָנווער און גלייַכן ביידע די טראַנסמיסיע רעזולטאַט ימפּידאַנס און די אַנטענע אַרייַנשרייַב ימפּידאַנס, די מאַקסימום מאַכט וועט זיין איבערגעגעבן צו די אַנטענע. אין דעם פאַל, די VSWR וועט זיין 1: 1 און די וואָולטידזש און די קראַנט וועט זיין קעסיידערדיק איבער די גאנצע לענג פון די קאָרמען ליניע.

1) VSWR קאַלקולאַטיאָן

צוריקקער אָנווער איז אַ מעסטן אין דב פון די פאַרהעלטעניש פון מאַכט אין די ינסידענט כוואַליע צו די אין די רעפלעקטעד כוואַליע, און מיר דעפינירן עס צו האָבן אַ נעגאַטיוו ווערט.

צוריקקער אָנווער = 10 קלאָץ (Pr / Pi) = 20 קלאָץ (ער / עי)

למשל, אויב אַ מאַסע האט אַ צוריקקער אָנווער פון -10 דב, 1/10 פון די ינסידענט מאַכט איז שפיגלט. די העכער די צוריקקער אָנווער, די ווייניקער מאַכט איז אַקשלי פאַרפאַלן.

די מיסמאַטש אָנווער איז אויך וויכטיק. דאָס איז אַ מעסטן פון ווי פיל די טראַנסמיטטעד מאַכט איז אַטטענואַטעד רעכט צו אָפּשפּיגלונג. עס איז געגעבן דורך די פאלגענדע שייכות:

מיסמאַטש אָנווער = 10 קלאָץ (1-פּ 2)

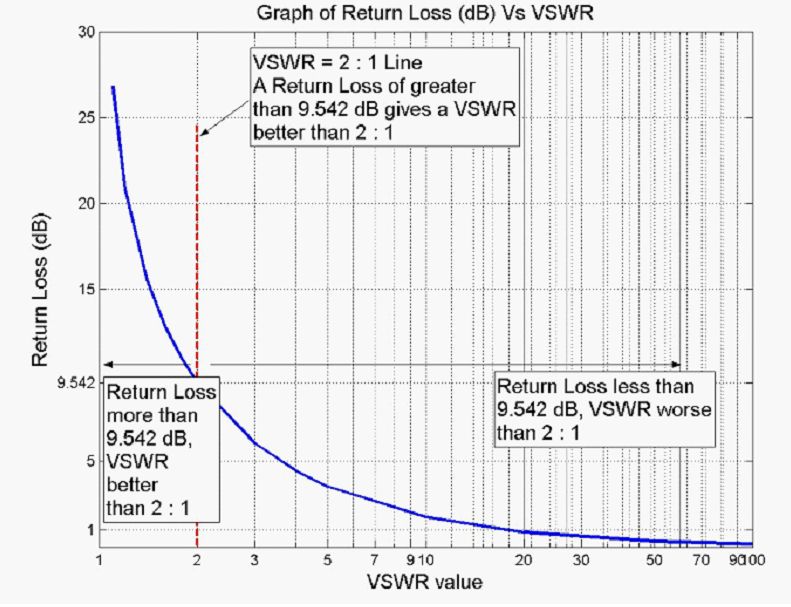
למשל, פֿון טאַבלע 1 אַן אַנטענע מיט אַ VSWR פון 2: 1 וואָלט האָבן אַ אָפּשפּיגלונג קאָואַפישאַנט פון 0.333, אַ מיסמאַטש אָנווער פון -0.51 דב, און אַ צוריקקער אָנווער פון -9.54 דב (11% פון דיין טראַנסמיטער מאַכט איז שפיגלט צוריק. )

2) Free VSWR קאַקולאַטיאָן טשאַרט

דאָ ס אַ פּשוט VSWR כעזשבן טשאַרט. 

געדענקט שטענדיק אַז VSWR זאָל זיין אַ נומער גרעסער ווי 1.0
ווסוור	רעפלעקטיאָן קאָואַפישאַנט (Γ)	רעפלעקטעד מאַכט (%)	וואָולטידזש אָנווער	רעפלעקטעד מאַכט (דב)	צוריקקער אָנווער	מיסמאַטש אָנווער (דב)
1	0.00	0.00	0	-ונפיניטי	ומענדיקייַט	0.00
1.15	0.070	0.5	7.0	-קסנומקס	23.13	0.021
1.25	0.111	1.2	11.1	-קסנומקס	19.08	0.054
1.5	0.200	4.0	20.0	-קסנומקס	13.98	0.177
1.75	0.273	7.4	קסנומקס.	-קסנומקס	11.29	0.336
1.9	0.310	9.6	31.6	-קסנומקס	10.16	0.440
2.0	0.333	11.1	33.3	-קסנומקס	9.540	0.512
2.5	0.429	18.4	42.9	-קסנומקס	7.360	0.881
3.0	0.500	25.0	50.0	-קסנומקס	6.021	1.249
3.5	0.555	30.9	55.5	-קסנומקס	5.105	1.603
4.0	0.600	36.0	60.0	-קסנומקס	4.437	1.938
4.5	0.636	40.5	63.6	-קסנומקס	3.926	2.255
5.0	0.666	44.4	66.6	-קסנומקס	3.522	2.553
10	0.818	66.9	81.8	-קסנומקס	1.743	4.807
20	0.905	81.9	90.5	-קסנומקס	0.8693	7.413
100	0.980	96.1	98.0	-קסנומקס	0.1737	14.066
...	...	...	...	...	...	...
∞	∞	100	100	∞	∞	∞
עקסטרע רידינג: VSWR אין אַנטענע די VSWR (Voltage Standing Wave Ratio) איז אַן אָנווייַז פון די סומע פון ​​מיסמאַטשאַס צווישן אַן אַנטענע און די קאָרמען ליניע צו אים. דאָס איז אויך באַוווסט ווי די Standing Wave Ratio (SWR). די קייט פון וואַלועס פֿאַר VSWR איז פֿון 1 צו ∞.  א VSWR ווערט אונטער 2 איז גערעכנט ווי פּאַסיק פֿאַר רובֿ אַנטענע אַפּלאַקיישאַנז. די אַנטענע קענען זיין דיסקרייבד ווי אַ "גוטע גלייַכן". אַזוי ווען עמעצער זאגט אַז די אַנטענע איז שוואַך מאַטשט, זייער אָפט עס מיטל אַז די VSWR ווערט יקסידז 2 פֿאַר אַ אָפטקייַט פון אינטערעס.  צוריקקער אָנווער איז אן אנדער ספּעציפיצירן ספּעציפיצירן און איז באדעקט מער דעטאַל אין די אָפּטיילונג פֿאַר אַנטענע טעאָריע. א קאַנווענשאַנאַל פארלאנגט קאַנווערזשאַן איז צווישן צוריקקער אָנווער און VSWR, און עטלעכע וואַלועס זענען טאַבולאַטעד אין די טשאַרט, צוזאַמען מיט אַ גראַפיק פון די וואַלועס פֿאַר שנעל דערמאָנען.

פֿון וואַנען נעמען זיך די חשבונות? נו, אָנהייבן מיט די פאָרמולע פֿאַר VSWR:

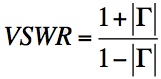
אויב מיר יבערקערן די פאָרמולע, מיר קענען רעכענען די אָפּשפּיגלונג קאָואַפישאַנט (אָדער צוריקקער אָנווער, s11) פֿון די VSWR:

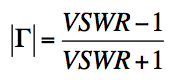
דער אָפּשפּיגלונג קאָואַפישאַנט איז איצט דיפיינד אין טערמינען פון וואָולטידזש. מיר טאַקע ווילן צו וויסן ווי פיל מאַכט איז רעפלעקטעד. דעם וועט זיין פּראַפּאָרשאַנאַל צו די קוואַדראַט פון דעם וואָולטידזש (V ^ 2). דעריבער, די רעפלעקטעד מאַכט אין פּראָצענט וועט זיין:

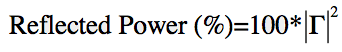
מיר קענען גער די רעפלעקטעד מאַכט צו דעסיבאַלז פשוט:

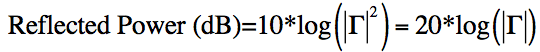
צום סוף, די מאַכט איז אָדער שפיגלט אָדער איבערגעגעבן צו די אַנטענע. די סומע צו די אַנטענע איז געשריבן ווי () און איז סימפּלי (1- ^ 2). דאָס איז באַוווסט ווי מיסמאַטש אָנווער. דאָס איז די סומע פון ​​מאַכט וואָס איז פאַרפאַלן רעכט צו ימפּידאַנס מיסמאַטש, און מיר קענען רעכענען די פערלי לייכט:

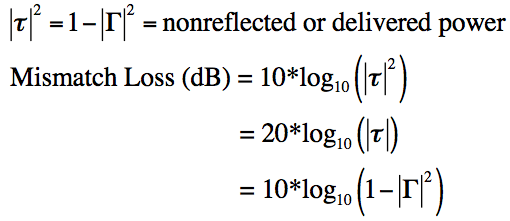
און דאָס איז אַלע וואָס מיר דאַרפֿן צו וויסן צווישן VSWR, s11 / return loss און מיסמאַטש אָנווער. איך האָפן אַז איר האָט ווי גרויס צייט ווי איך געהאט.

קאָנווערסיאָן טיש - dBm צו dBW און W (וואט)

אין דעם טאַבלע, מיר פאָרשטעלן ווי די ווערט פון מאַכט אין dBm, dBW און Watt (W) קאָראַספּאַנדינג צו יעדער אנדערער.

מאַכט (דבם)	מאַכט (דבוו)	מאַכט ((וו) וואט)
100	70	10 MW
90	60	1 MW
80	50	100 קוו
70	40	10 קוו
60	30	1 קוו
50	20	קסנומקס וו
40	10	קסנומקס וו
30	0	קסנומקס וו
20	-קסנומקס	קסנומקס מוו
10	-קסנומקס	קסנומקס מוו
0	-קסנומקס	קסנומקס מוו
-קסנומקס	-קסנומקס	100 μ וו
-קסנומקס	-קסנומקס	10 μ וו
-קסנומקס	-קסנומקס	1 μ וו
-קסנומקס	-קסנומקס	100 נ.וו.
-קסנומקס	-קסנומקס	10 נ.וו.
-קסנומקס	-קסנומקס	1 נ.וו.
-קסנומקס	-קסנומקס	100 פּוו
-קסנומקס	-קסנומקס	10 פּוו
-קסנומקס	-קסנומקס	1 פּוו
-קסנומקס	-קסנומקס	0.1 פּוו
-∞	-∞	קסנומקס וו
ווו: dBm = דעסיבעל-מילליוואַט דבוו = דעסיבעל-וואט מוו = מעגאַוואַט קוו = קילאוואט וו = וואט מוו = מילליוואַט μ וו = מיקראָוואַט נוו = נאַנאָוואַט פּוו = פּיקאָוואַטט

▲צוריק▲

3) VSWR פאָרמולע

דער פּראָגראַם איז אַ אַפּלאַט פֿאַר קאַלקיאַלייטינג די VSVR פאַרהעלטעניש וואָולטידזש שטייענדיק וואַווע.

ווען איר שטעלן אַ אַנטענע און טראַנסמיטער סיסטעם, עס איז וויכטיק צו ויסמיידן ימפּידאַנס מיסמאַטשינג ערגעץ אין די סיסטעם. קיין מיסמאַטש מיטל עטלעכע פּראָפּאָרציע פון ​​די רעזולטאַט כוואַליע איז שפיגלט צוריק צו די טראַנסמיטער און די סיסטעם ווערט באַטלאָניש. מיסמאַטטשעס קענען פּאַסירן ביי ינטערפייסיז צווישן פאַרשידן עקוויפּמענט, למשל טראַנסמיטער, קאַבלע און אַנטענע. אַנטענאַז האָבן ימפּידאַנס, וואָס איז יוזשאַוואַלי 50 אָום (ווען אַנטענע איז די ריכטיק דימענשאַנז). ווען אָפּשפּיגלונג אַקערז, שטייענדיק כוואליעס זענען געשאפן אין די קאַבלע.

VSWR פאָרמולע און אָפּשפּיגלונג קאָואַפישאַנט:

עק 1	אָפּשפּיגלונג קאָואַפישאַנט Γ איז דיפיינד ווי	עק 2	די VSWR אָדער וואָולטידזש שטייענדיק כוואַליע פאַרהעלטעניש
פאָרמולע		פאָרמולע
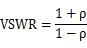גאַמאַ	ZL = די ווערט אין אָומז פון די מאַסע (טיפּיקלי אַן אַנטענע) Zo = די כאַראַקטעריסטיש ימפּידאַנס פון די טראַנסמיסיע שורה אין אָומז	Sigma	געגעבן אַז ρ וועט בייַטן פון 0 צו 1, די קאַלקיאַלייטיד וואַלועס פֿאַר VSWR וועט זיין פֿון 1 ביז ומענדיקייַט.
קאַלקיאַלייטיד וואַלועס	צווישן -1 ≦ Γ ≦ 1.	קאַלקיאַלייטיד וואַלועס	1 אָדער אַ 1: 1 פאַרהעלטעניש.
ווען ווערט איז "-1".	מיטל 100% אָפּשפּיגלונג אַקערז און קיין מאַכט איז טראַנספערד צו די מאַסע. די שפיגלט כוואַליע איז 180 דיגריז אויס פון פאַסע (ינווערטיד) מיט די אינצידענט כוואַליע.	מיט עפן קרייַז	דאָס איז אַן אָפן קרייַז צושטאַנד אָן אַנטענע פארבונדן. עס מיטל אַז ZL איז ינפאַנאַט און די טערמינען Zo וועט פאַרשווינדן אין עק .1, אַזוי אַז Γ = 1 (100% אָפּשפּיגלונג) און ρ = 1. קיין מאַכט איז טראַנספערד און VSWR וועט זיין ינפאַנאַט.
ווען ווערט איז “1”.	מיטל 100% אָפּשפּיגלונג אַקערז און קיין מאַכט איז טראַנספערד צו די מאַסע. די שפיגלט כוואַליע איז אין פאַסע מיט די אינצידענט כוואַליע.	מיט קורץ קרייַז	ימאַדזשאַן אַז די קאַבלע האט אַ קורץ קרייַז. עס מיטל אַז ZL איז 0 און Eq.1 וועט רעכענען Γ = -1 און ρ = 1. קיין מאַכט איז טראַנספערד און VSWR איז ינפאַנאַט.
ווען ווערט איז “0”.	מיטל קיין אָפּשפּיגלונג אַקערז און אַלע מאַכט איז טראַנספערד צו די מאַסע. (IDEAL)	מיט אַנטענעד ריכטיק.	ווען אַ ריכטיק מאַטשט אַנטענע איז פארבונדן, אַלע ענערגיע איז טראַנספערד צו די אַנטענע און איז קאָנווערטעד צו ראַדיאַציע. ZL איז 50 אָום און Eq.1 וועט רעכענען Γ צו זיין נול. אַזוי VSWR וועט זיין פּונקט 1.
ען / א	ען / א	מיט אַנטרין גלייך מאַטשט.	ווען אַ ינקערעקטלי מאַטשט אַנטענע איז פארבונדן, די ימפּידאַנס וועט ניט מער זיין 50 אָום און אַ ימפּידאַנס מיסמאַטש אַקערז און אַ טייל פון די ענערגיע איז שפיגלט צוריק. די סומע פון ​​די שפיגלט ענערגיע דעפּענדס אויף די הייך פון די מיסמאַטש און די VSWR וועט זיין אַ ווערט העכער 1.
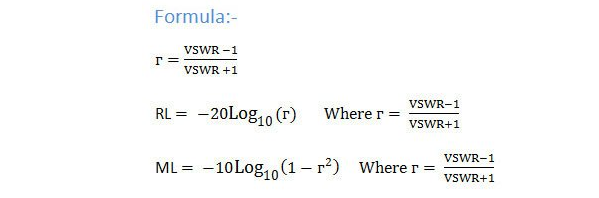
ווען ניצן קאַבלע פון ​​פאַלש קוואַליטעט ימפּידאַנס די קאַבלע / טראַנסמיסיע שורה געניצט צו פאַרבינדן די אַנטענע צו די טראַנסמיטער דאַרף זיין די ריכטיק כאַראַקטער ימפּידאַנס Zo.  טיפּיקאַללי, קאָאַקסיאַל קייבאַלז זענען 50 אָהמס (75 אָהמס פֿאַר טעלאַוויזשאַנז און סאַטעליט) און זייער וואַלועס זענען געדרוקט אויף די קייבאַלז זיך.  די סומע פון ​​ענערגיע רעפלעקטעד דעפּענדס אויף די מדרגה פון די מיסמאַטש, און אַזוי VSWR וועט זיין אַ ווערט העכער 1.

איבערבליק:

וואָס זענען שטייענדיק כוואליעס? א מאַסע איז פארבונדן צו די סוף פון די טראַנסמיסיע שורה און דער סיגנאַל פלאָוז צוזאמען עס און גייט אריין די מאַסע. אויב די מאַסע ימפּידאַנס טוט נישט גלייַכן די טראַנסמיסיע שורה ימפּידאַנס, טייל פון די טראַוואַלינג כוואַליע איז שפיגלט צוריק צו דער מקור.

ווען אָפּשפּיגלונג אַקערז, די אַרומפאָרן צוריק אַראָפּ די טראַנסמיסיע שורה און קאַמביינד מיט די ינסידענט כוואליעס צו פּראָדוצירן שטייענדיק כוואליעס. עס איז וויכטיק צו באַמערקן אַז די ריזאַלטינג כוואַליע איז סטיישאַנערי ווי און טוט נישט פאַרמערן ווי אַ נאָרמאַל כוואַליע און נישט אַריבערפירן ענערגיע צו די מאַסע. די כוואַליע האט געביטן פון מאַקסימום און מינימום אַמפּליטוד גערופן אַנטי-נאָודז און נאָודז ריספּעקטיוולי.

ווען קאַנעקטינג די אַנטענע, אויב אַ VSWR פון 1.5 איז געשאפן, די מאַכט עפעקטיווקייַט איז 96%. ווען אַ VSWR פון 3.0 איז געשאפן, די מאַכט עפעקטיווקייַט איז 75%. אין פאַקטיש נוצן, עס איז נישט רעקאַמענדיד צו יקסיד אַ VSWR פון 3.

▲צוריק▲

5. ווי אַזוי מעסטן די שטייענדיק כוואַליע פאַרהעלטעניש - וויקיפּעדיע דערקלערונג
פילע פאַרשידענע מעטהאָדס קענען ווערן גענוצט צו מעסטן די שטייענדיק כוואַליע פאַרהעלטעניש. די מערסט ינטואַטיוו מעטהאָדס ניצט אַ שפּעלטל ליניע, וואָס איז אַ אָפּטיילונג פון טראַנסמיסיע שורה מיט אַן אָפֿן שפּעלטל וואָס אַלאַוז אַ זאָנד צו דיטעקט די פאַקטיש וואָולטידזש אין פאַרשידענע פונקטן צוזאמען די שורה. 

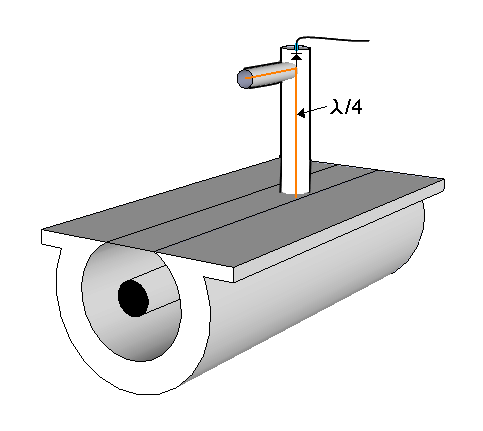
אַזוי די מאַקסימום און מינימום וואַלועס קענען זיין קאַמפּערד גלייַך. דעם אופֿן איז געניצט אין ווהף און העכער פריקוואַנסיז. אין נידעריקער פריקוואַנסיז, אַזאַ שורות זענען ימפּראַקטאַקלי לאַנג. דירעקטיאָנאַל קאַפּלערז קענען זיין געוויינט ביי HF דורך מייקראַווייוו פריקוואַנסיז. 

עטלעכע זענען XNUMX/XNUMX כוואַליע אָדער מער לאַנג, וואָס ריסטריקץ זייער נוצן צו די העכער פריקוואַנסיז. אנדערע טייפּס פון דירעקטיאָנאַל קאַפּלערז מוסטער די קראַנט און וואָולטידזש אין אַ איין פונט אין די טראַנסמיסיע דרך און מאַטאַמאַטיקאַללי פאַרבינדן זיי אין אַזאַ אַ וועג צו פאָרשטעלן די מאַכט פלאָוינג אין איין ריכטונג.

דער פּראָסט טיפּ פון SWR / מאַכט מעטער געניצט אין ליבהאָבער אָפּעראַציע קען אַנטהאַלטן אַ צווייענדיק דירעקטיאָנאַל קאַפּלער. אנדערע טייפּס נוצן אַ איין קאַפּלער וואָס קענען זיין ראָוטייטיד 180 דיגריז צו פּרובירן די מאַכט פלאָוינג אין יעדער ריכטונג. ונידירעקטיאָנאַל קאַפּערז פון דעם טיפּ זענען בארעכטיגט פֿאַר פילע אָפטקייַט ריינדזשאַז און מאַכט לעוועלס און מיט צונעמען קאַפּלינג וואַלועס פֿאַר די אַנאַלאָג מעטער.

א דירעקטיאָנאַל וואַטטמעטער ניצן אַ דריי-רידעראַבאַל דירעקטיאָנאַל קאַפּלער עלעמענט

די פֿאָרווערטס און שפיגלט מאַכט געמאסטן דורך דירעקטיאָנאַל קאַפּערז קענען ווערן גענוצט צו רעכענען SWR. די קאַמפּיאַטיישאַנז קענען זיין מאַטאַמאַטיקאַללי אין אַנאַלאָג אָדער דיגיטאַל פאָרעם אָדער ניצן גראַפיקאַל מעטהאָדס געבויט אין די מעטער ווי אַ נאָך וואָג אָדער דורך לייענען פֿון די אַריבער פונט צווישן צוויי נעעדלעס אויף דער זעלביקער מעטער.

די אויבן מעאַסורינג ינסטראַמאַנץ קענען זיין געוויינט "אין שורה", דאָס הייסט, די פול מאַכט פון די טראַנסמיטער קענען פאָרן דורך די מעאַסורינג מיטל צו לאָזן קעסיידערדיק מאָניטאָרינג פון SWR. אנדערע ינסטראַמאַנץ, אַזאַ ווי נעץ אַנאַליזערס, דירעקטיאָנאַל קאַפּלערז מיט נידעריק מאַכט און אַנטענע בריקן נוצן נידעריק מאַכט פֿאַר די מעזשערמאַנט און מוזן זיין פארבונדן אין פּלאַץ פון די טראַנסמיטער. בריק סערקאַץ קענען ווערן גענוצט צו גלייַך מעסטן די פאַקטיש און ויסגעטראַכט טיילן פון אַ מאַסע ימפּידאַנס און צו נוצן די וואַלועס צו אַרויספירן SWR. די מעטהאָדס קענען צושטעלן מער אינפֿאָרמאַציע ווי בלויז SWR אָדער פֿאָרווערטס און שפיגלט מאַכט. [11] שטיי אַליין אַנטענע אַנאַליזערס נוצן פאַרשידן מעאַסורינג מעטהאָדס און קענען אַרויסווייַזן SWR און אנדערע פּאַראַמעטערס פּלאָטעד קעגן אָפטקייַט. דורך דירעקטיאָנאַל קאַפּלערז און אַ בריק אין קאָמבינאַציע, עס איז מעגלעך צו מאַכן אַ שורה קיילע וואָס לייענט גלייַך אין קאָמפּלעקס ימפּידאַנס אָדער SWR. [12] שטיין אַליין אַנטענע אַנאַליזערס זענען אויך בנימצא וואָס מעסטן קייפל פּאַראַמעטערס.

▲צוריק▲

6. אָפט פרעגן פֿראגן

1) וואָס ז הויך VSWR?

אויב די VSWR איז צו הויך, עס קען זיין צו פיל ענערגיע רעפלעקטעד אין אַ מאַכט אַמפּלאַפייער, וואָס קען שעדיקן די ינערלעך קרייַז. אין אַן אידעאל סיסטעם, עס וואָלט זיין אַ VSWR פון 1: 1. סיבות פון אַ הויך ווסוור ראַנג קען זיין די נוצן פון אַ ימפּראַפּער מאַסע אָדער עפּעס אומבאַקאַנט אַזאַ ווי אַ דאַמידזשד טראַנסמיסיע שורה.

2) ווי טאָן איר רעדוצירן VSWR?

איין טעכניק צו רעדוצירן די רעפלעקטעד סיגנאַל פֿון די ינפּוט אָדער רעזולטאַט פון קיין מיטל איז צו שטעלן אַן אַטטענואַטאָר איידער אָדער נאָך די מיטל. די אַטטענואַטאָר ראַדוסאַז די שפיגלט סיגנאַל צוויי מאָל די ווערט פון די אַטטענואַטיאָן, בשעת די טראַנסמיטטעד סיגנאַל נעמט די נאָמינאַל אַטטענואַטיאָן ווערט. (עצות: צו דרוקן ווי וויכטיק VSWR און RL זענען פֿאַר דיין נעץ, באַטראַכטן אַ רעדוקציע אין פאָרשטעלונג פון VSWR פון 1.3: 1 צו 1.5: 1 - דאָס איז אַ ענדערונג אין Return Loss פון 16 dB צו 13 dB).

3) איז ס 11 צוריקקער אָנווער?

אין פיר, די מערסט אָפט ציטירט פּאַראַמעטער וועגן אַנטענאַז איז S11. ס 11 רעפּראַזענץ ווי פיל מאַכט איז רעפלעקטעד פֿון די אַנטענע, און דעריבער איז באַוווסט ווי דער אָפּשפּיגלונג קאָואַפישאַנט (מאל געשריבן ווי גאַמאַ: אָדער צוריקקער אָנווער... דעם אנגענומען מאַכט איז אָדער ראַדיאַטעד אָדער אַבזאָרבד ווי לאָססעס ין דער אַנטענע.

4) פארוואס מעסטן VSWR?

VSWR (Voltage Standing Wave Ratio), איז אַ מעסטן פון ווי יפעקטיוולי ראַדיאָ-אָפטקייַט מאַכט איז טראַנסמיטטעד פֿון אַ מאַכט מקור, דורך אַ טראַנסמיסיע שורה, אין אַ מאַסע (פֿאַר בייַשפּיל פון אַ מאַכט אַמפּלאַפייער דורך אַ טראַנסמיסיע שורה צו אַן אַנטענע) . אין אַן אידעאל סיסטעם, 100% פון די ענערגיע איז טראַנסמיטטעד.

5) ווי אַזוי קען איך פאַרריכטן High VSWR?

אויב דיין אַנטענע איז מאָונטעד אַראָפּ נידעריק אויף די פאָרמיטל, ווי אויף די באַמפּער אָדער הינטער אַ טאַקסי קאַב, דער סיגנאַל קענען אָפּשפּרונג צוריק צו דער אַנטענע און קאָזינג אַ הויך SWR. צו פאַרגיכערן דעם, האַלטן לפּחות די שפּיץ 12 אינטשעס פון דער אַנטענע אויבן די דאַך שורה און שטעלן די אַנטענע ווי הויך ווי מעגלעך אויף די פאָרמיטל.

6) וואָס איז אַ גוטע VSWR רידינג?
דער בעסטער לייענען מעגלעך איז 1.01: 1 (46 דב צוריקקער אָנווער), אָבער יוזשאַוואַלי אַ לייענען אונטער 1.5: 1 איז פּאַסיק. אַרויס די שליימעסדיק וועלט, אַ 1.2: 1 (20.8 דב צוריקקער אָנווער) איז מערסטנס אָנווענדלעך. צו ענשור אַ פּינטלעך לייענען, עס איז בעסטער צו פאַרבינדן די מעטער אין דער באַזע פון ​​די אַנטענע.

7) איז 1.5 SWR גוט?
יא עס איז! די ידעאַל קייט איז SWR 1.0-1.5. עס איז פּלאַץ פֿאַר פֿאַרבעסערונג ווען SWR 1.5 - 1.9, אָבער SWR אין דעם קייט זאָל נאָך צושטעלן טויגן פאָרשטעלונג. טייל מאָל, ווייַל פון ינסטאַליישאַנז אָדער פאָרמיטל וועריאַבאַלז, עס איז אוממעגלעך צו באַקומען SWR נידעריקער ווי דעם.

8) ווי טאָן איך קאָנטראָלירן מיין SWR אָן אַ מעטער?
דאָ זענען די סטעפּס צו ניגן אַ CB ראַדיאָ אָן אַ SWR מעטער:
1) געפֿינען אַ שטח מיט לימיטעד ינטערפיראַנס.
2) מאַכט זיכער אַז איר האָט אַן נאָך ראַדיאָ.
3) ניגן ביידע ראַדיאָס צו דער זעלביקער קאַנאַל.
4) רעדן אין איין ראַדיאָ און הערן דורך די אנדערע.
5) מאַך איין ראַדיאָ אַוועק און טאָן ווען דער געזונט איז קלאָר.
6) סטרויערן דיין אַנטענע ווי איר דאַרפֿן.

9) צי אַלע CB אַנטענאַז דאַרפֿן צו זיין טונד?
בשעת אַנטונינג טונינג איז נישט פארלאנגט צו אַרבעטן דיין קב סיסטעם, עס זענען עטלעכע וויכטיק סיבות וואָס איר זאָל שטענדיק סטרויערן אַן אַנטענע: ימפּראָוועד פאָרשטעלונג - אַ רעכט טונד אַנטענע וועט שטענדיק אַרבעט מער יפישאַנטלי ווי אַן אַנטונדיד אַנטענע.

10) פארוואס גייט מיין SWR אַרויף ווען איך רעדן?

איינער פון די מערסט פּראָסט סיבות פון הויך SWR רידינגז איז ינקערעקטלי קאַנעקטינג דיין SWR מעטער צו דיין ראַדיאָ און אַנטענע. ווען ינקערעקטלי אַטאַטשט, רידינגז וועט זיין געמאלדן ווי גאָר הויך, אפילו אויב אַלץ איז אינסטאַלירן בישליימעס. ביטע זען דעם אַרטיקל וועגן ינשורינג דיין SWR מעטער איז רעכט אינסטאַלירן.

7. בעסטער פריי אָנליין VSWR קאַלקולאַטאָר אין 2021

https://www.microwaves101.com/calculators/872-vswr-calculator
http://rfcalculator.mobi/vswr-forward-reverse-power.html
https://www.everythingrf.com/rf-calculators/vswr-calculator
https://www.pasternack.com/t-calculator-vswr.aspx
https://www.antenna-theory.com/definitions/vswr-calculator.php
http://www.flexautomotive.net/flexcalc/VSWR2/VSWR.aspx
https://www.allaboutcircuits.com/tools/vswr-return-loss-calculator/
http://www.csgnetwork.com/vswrlosscalc.html
https://www.ahsystems.com/EMC-formulas-equations/VSWR.php
http://cgi.www.telestrian.co.uk/cgi-bin/www.telestrian.co.uk/vswr.pl
https://www.changpuak.ch/electronics/calc_14.php
https://chemandy.com/calculators/return-loss-and-mismatch-calculator.htm
https://www.atmmicrowave.com/calculator/vswr-calculator/
http://www.emtalk.com/vswr.php

▲צוריק▲

ייַנטיילונג איז קאַרינג!

לאז איבער א מעלדונג 

אַרטיקל ליסטע